はじめに:矛盾を内包する論理と量子の世界
量子力学の世界では、粒子が同時に複数の状態に存在したり、離れた粒子同士が瞬時に影響し合ったりと、私たちの日常的な直観に反する現象が次々と観測されています。こうした量子特有の振る舞いを、従来の古典論理では十分に記述できないという問題が長年指摘されてきました。
一方、論理学の分野では「パラコンシステント論理」と呼ばれる、矛盾を許容しながらも論理体系全体が崩壊しない独特な論理が発展してきました。この論理体系と量子もつれの間には、興味深い形式的対応関係が存在することが近年の研究で明らかになっています。
本記事では、パラコンシステント論理の基本概念から、量子もつれとの理論的接点、そして量子計算への応用まで、学際的な視点から解説していきます。
パラコンシステント論理とは:爆発原理を拒否する論理体系
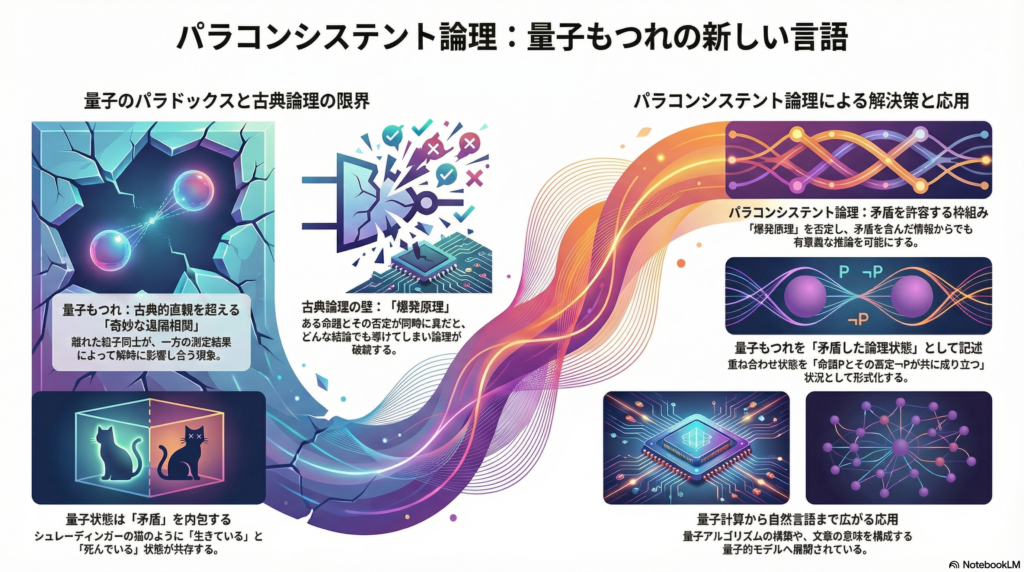
古典論理の限界と爆発原理
古典論理では、ある命題Pとその否定¬Pの両方が真であると仮定すると、「爆発原理」が働きます。これは、矛盾から任意の命題が導出できてしまうという原理で、論理体系全体が無意味化してしまいます。
パラコンシステント論理は、この爆発原理を禁止することで、矛盾を含む情報を扱っても有意義な推論を継続できる非古典的論理です。ニュートン・ダ・コスタやグレアム・プリーストらの先駆的研究により提唱され、現在では複数の体系が発展しています。
主要な体系と応用分野
代表的な体系として、ダ・コスタによるCn系列や、プリーストのLogic of Paradox(LP)があります。また、ウォルター・カルニエリらによる形式的不整合性の論理(LFI)では、命題に「その命題が整合的かどうか」の情報を付与する注釈付き論理も提案されています。
これらは自己言及的パラドックスを含む真理論や、矛盾データを含む知識ベースの形式的記述に活用されており、人工知能や情報工学の分野でも注目を集めています。
量子もつれの特徴:非局所的相関とパラドックス
量子もつれとは何か
量子もつれ(エンタングルメント)は、複数の粒子系が相互に強い相関を持っている状態を指します。もつれ状態では各粒子の性質が個別には確定せず、一方の粒子を測定すると他方の粒子が即座に相関した結果を示すという、古典的直観に反する現象が生じます。
例えば、スピンのもつれた電子対では、一方のスピンを測定して「上向き」が観測されると、もう一方は距離に関係なく瞬時に「下向き」に定まります。この非局所的な相関は、EPRパラドックスやベルの定理に示されるように、局所実在論と因果律への根本的な挑戦となりました。
古典論理から見たパラドックス性
古典論理の観点から見ると、もつれ状態は一種のパラドックスを孕んでいます。各粒子が測定されるまで「状態が確定していない」と同時に「相手と強い相関で結ばれている」という状況は、「粒子Aのスピンが上であり、かつ上ではない」かのような矛盾した記述とも解釈できます。
シュレーディンガーの猫の思考実験も同様に、「猫が生きている」と「猫が死んでいる」という矛盾する命題が同時に成り立つかのような状態を想定しています。古典論理ではこれは矛盾ですが、パラコンシステント論理ならこの両立する真理値を表現可能です。
パラコンシステント論理による量子もつれの記述
形式的類似性の発見
量子もつれや量子重ね合わせ状態の形式的性質は、パラコンシステント論理モデルと構造的に類似していることが指摘されています。もつれた量子状態を記述する際、各粒子の属性に対し古典的に定値を割り当てようとすると矛盾に突き当たる場合があります。
パラコンシステント論理では、そうした矛盾的情報を含む状態を扱っても破綻しないため、量子もつれの論理記述に適した枠組みを提供し得るのです。実際、研究者の間では「量子もつれに本質的な非整合性が存在すると受け入れるなら、その基盤論理はパラコンシステントであるべきだ」との議論が進められています。
多値論理による表現
具体的なモデルとしては、真理値が「真」「偽」「両方真(矛盾)」「どちらでもない(空)」の四値を持つベルナップの四値論理を用い、もつれ状態を各粒子の命題が「真かつ偽」と評価される状態として表現するアイデアがあります。
例えば、粒子1のスピンに関する命題Pと粒子2のスピンに関する命題Qを考えると、もつれ状態では個別にはPもその否定も確定しませんが、PとQの間には強い相関関係が存在します。この状況を、パラコンシステント論理では特殊な論理結合子や真理値表で表現できるのです。
量子力学への応用:理論から計算まで
ダ・コスタとデ・ロンデによる量子解釈
ニュートン・ダ・コスタは南米におけるパラコンシステント論理の開拓者で、ボーアの原子模型や旧量子論が理論内部に矛盾を含むことに着目しました。彼はパラコンシステント論理を用いて「科学における矛盾理論」を形式化できることを示しています。
哲学者クリスチャン・デ・ロンデとの共同研究では、2013年に「量子重ね合わせのパラコンシステント論理(PAQS)」を提案し、量子測定問題において測定前の系の状態を「命題Pかつその否定が成り立つような論理的状況」と捉え、その矛盾を許容することで量子力学を再解釈する可能性を論じました。
この提案に対しては、ジョナス・アーレハートとデシオ・クラウゼらから批判もなされましたが、デ・ロンデは2019年の論文で反論を展開し、現在も議論が続いています。
パラコンシステント・チューリングマシンと量子計算
計算機科学の観点からは、ウォルター・カルニエリらのグループが量子計算をパラコンシステント論理でエミュレートする研究を行っています。彼らは非決定性チューリング機械の計算過程を公理的に表現しようと試みたところ、古典論理の下ではその理論が矛盾を含むことを発見しました。
しかし基盤の論理をパラコンシステント論理に置き換えることで、矛盾を含む計算状態を扱える計算モデルを構築することに成功しています。このモデルでは、量子計算で特徴的な重ね合わせ状態をパラコンシステントな論理状態として部分的に再現でき、ドイチュの問題などを解く「パラコンシステント・アルゴリズム」が提案されています。
エンタングルメントを表す論理結合子
さらに改良版では、新たな論理結合子として「エンタングルメント」を表す接続子を導入し、論理式のレベルで「状態pとqがエンタングルしている」ことを記述できるようになりました。この接続子⊗を用いてp⊗qと書けば「命題pとqがもつれた関係にある」という論理式となります。
興味深いことに、この論理モデルでは構造規則の制限が鍵となっています。論理シーケント計算において縮約や弱化といった構造ルールを認めないことで、量子計算の「ノー・クローニング」や「消去不可」という制約を自然に反映しています。これは線形論理にも通じる発想で、リソース管理を厳密に行う論理構造の中で量子の並列性を表現しようとするものです。
量子論理と他の非古典的論理との関係
量子論理の位置づけ
量子力学の命題構造を記述する論理体系として、1936年にバーコフとフォン・ノイマンが提唱した量子論理は、古典論理と直観主義論理に次ぐ第三の論理体系として歴史的に重要です。
量子論理では、物理系の測定に対応する射影命題の集合が直交完備な正則束を成すとされます。これはブール代数とは異なり分配律が一般には成り立たないため、非分配型論理とも呼ばれます。ただし、各命題は最終的には真か偽のどちらかに決定されるため、基本的には二値的です。
直観主義論理との接点
直観主義論理は排中律を認めない構成主義的論理ですが、一部の研究者は量子力学の「測定まで命題の真偽が決まらない」状況を将来事象の不確定性と関連づけ、直観主義的量子論理を模索してきました。
オランダのロニー・ヘルメンスは弱直観主義的量子論理を提案し、射影演算子すべてではなく一部のみを命題に採用することで直観主義論理の分配的構造を維持しつつ量子現象を記述しようとしました。
様相論理と線形論理の役割
様相論理(モーダル論理)との接点も存在します。量子系では観測や時間発展による状態の変化を考える必要があり、可能世界の枠組みを用いる様相論理や動的論理が応用されています。量子ダイナミックロジックは古典プログラムの動的論理を発展させた枠組みで、量子プログラムやプロトコル中の状態遷移を記述します。
線形論理との関係では、量子計算機科学において重要な接点があります。線形論理は構造規則を制限し論理式の複製や削除を禁止する論理であり、これは量子情報のノー・クローニング定理や不可分性と親和的です。実際、量子プログラミング言語の設計では線形型システムを用いて量子ビットのコピー・破棄を防ぐ手法が一般的です。
意味論と認知科学への展開
分散表現意味論の量子的モデル
近年、自然言語の意味を量子情報の形式になぞらえて捉える動きが注目を集めています。ボブ・コーケらはカテゴリカル合成分散意味論(DisCoCat)を提唱し、文章の意味をベクトル空間上の状態と見立て、文法構造を線形写像として表現することで、量子力学の形式を言語意味に応用しました。
このモデルでは、単語の意味ベクトル同士が文章中でエンタングルして文全体の意味を構成します。語と語の間に生じる文脈的相互作用は、量子もつれによる相関と形式的に似通った構造で捉えられるのです。
量子認知科学の試み
量子認知科学の分野でも、ヒトの判断や概念の組み合わせに量子論的構造を見出す研究があります。ある概念と別の概念を組み合わせたときに各概念の属性が直和では説明できない振る舞いが観察される場合、これを古典確率ではなく量子確率モデルで説明する試みがなされています。
量子モデルでは概念がヒルベルト空間上の状態ベクトルで表され、概念の組み合わせはテンソル積状態として記述されます。人間の意思決定で見られる文脈効果や両立しえない信念の同時保持といった現象を、これらのモデルが説明する可能性があるのです。
まとめ:矛盾を内包する世界像への挑戦
パラコンシステント論理と量子もつれの対応関係に関する研究は、論理学・物理学・計算機科学・言語学といった異なる分野の学際的コラボレーションによって深化しています。
矛盾を許容しながらも破綻しない論理体系は、量子力学の非直観的現象に対して新たな解釈の可能性を提供しています。量子重ね合わせやもつれ状態を「矛盾を内包する状態」と捉えることで、測定問題や非局所性といった量子力学の根本的な謎に、論理学から光を当てる試みが進められているのです。
今後も、量子計算の論理的基礎づけや、自然言語処理への量子的アプローチなど、多様な応用が期待されます。これらの研究は最終的に、我々の現実理解と言語・情報処理の基盤に横たわる論理の在り方を再考させるものであり、「矛盾を内包しつつ破綻しない世界像」を追求する知的探究と言えるでしょう。
コメント