パラコンシステント論理と量子力学が示す非古典的世界
現代の論理学と物理学は、古典的な枠組みを超えた興味深い接点を見出しています。矛盾が生じても体系全体が崩壊しないパラコンシステント論理と、重ね合わせや非局所性といった反直観的現象を示す量子力学。一見異なる分野に見えるこれらの領域は、実は深い構造的共通性を持ち、人工知能や機械学習における新しい推論モデルの基盤として注目されています。
古典論理では、矛盾(命題Pとその否定¬Pが同時に真)が生じると「爆発原理」により、あらゆる命題が導出可能となり体系が無意味化します。しかし現実世界のデータベースや知識システムは、しばしば矛盾を含みます。同様に、量子系は測定前に複数の状態を同時に保持する重ね合わせを示し、古典的な「真か偽か」の二値論理では捉えきれません。
本記事では、これら二つの非古典的体系がどのように結びつき、AI推論システムにどのような革新をもたらす可能性があるのかを探ります。
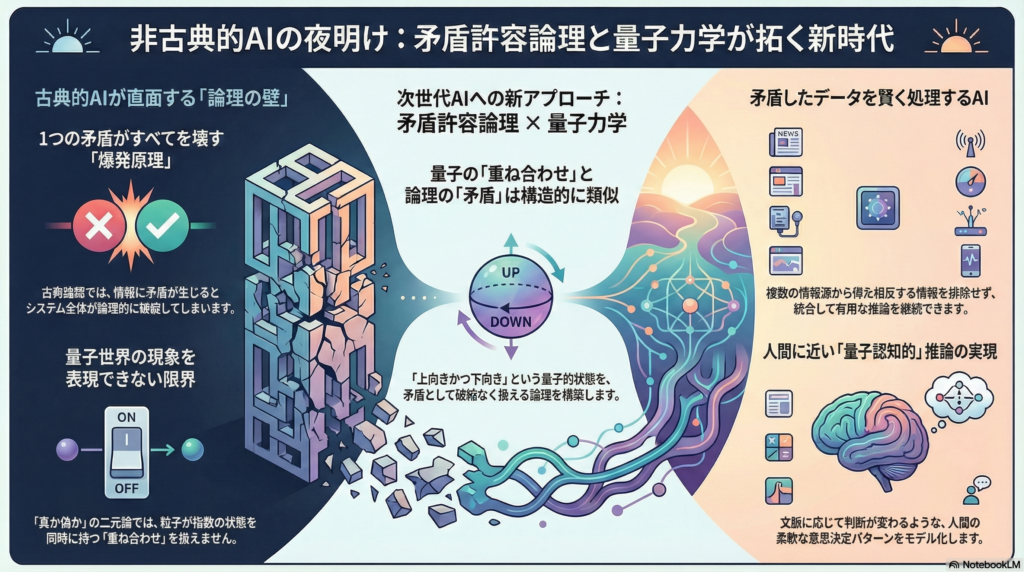
量子力学とパラコンシステント論理の構造的類似性
量子重ね合わせと矛盾の共存
量子力学における最も象徴的な現象の一つが重ね合わせです。測定前のスピン粒子は「上向き」と「下向き」の両方の状態を同時に持つとされます。この状況は、古典論理では矛盾とみなされる「PかつP」が非自明に成立する状態と類比的です。
パラコンシステント論理の創始者の一人であるNewton da Costaと哲学者Christian de Rondeは、量子重ね合わせを「矛盾を明示的に認める」アプローチで記述することを提案しました。彼らは「スピンが上であり、かつ下でもある」という矛盾的記述を、爆発原理を回避しながら扱える論理体系の構築を目指しました。これは、古典論理に量子現象を無理に適合させるのではなく、論理体系そのものを量子の性質に合わせて変更するという根本的な転換です。
非可換性と論理構造の対応
量子力学では、測定する順序によって結果が変わる非可換性が重要な特徴です。可観測量AとBについて、一般に[A, B] ≠ 0が成立します。これは古典論理におけるAND/ORの可換性とは対照的です。
ビルコフとフォン・ノイマンが提唱した量子論理では、分配法則が破れることが知られています。同様に、パラコンシステント論理や関連性論理の一部は、古典論理の構造的性質を満たしません。量子命題の格子構造では、どちらの選言肢も真でなくても選言命題が真になるケースがあり、排中律からの逸脱が観察されます。
量子非局所性とベルの定理が示唆する論理的課題
エンタングルした粒子対は、ベルの定理が示すように、古典的な局所的隠れ変数モデルでは説明できない相関を示します。この現象を古典的ブール論理の枠内で理解しようとすると、理論的矛盾が生じます。
一部の研究者は、こうした矛盾を単に排除するのではなく、論理的に「矛盾として扱う」ことを提案しています。パラコンシステント論理は、古典的観点からは矛盾した命題を含みながらも、推論システム全体は破綻しない枠組みを提供します。これにより、量子非局所性がもたらす概念的困難に新たな視点を与える可能性があります。
相補性原理とパラコンシステント的記述
ボーアの相補性原理が示す波動性と粒子性の両立も、古典論理では扱いにくい概念です。電子が「粒子的性質と波動的性質の両方を示す」という記述は、古典論理では矛盾ですが、量子理論では受け入れられています。
パラコンシステント論理では、命題Aとその否定¬Aが非自明に共存する形で相補性を定式化できます。近年の研究では、量子力学の基底論理としてパラコンシステント論理を採用することで、補完的またはエンタングルした性質を「共存する命題」として整合的に扱おうとする試みがなされています。
パラコンシステント量子論理の構築と理論的発展
初期の形式化:Dalla ChiaraとGiuntiniの貢献
1980年代、イタリアの研究者Dalla ChiaraとGiuntiniは、量子命題が古典的矛盾律を破る可能性を許容するパラコンシステント量子論理を構築しました。彼らの体系は、標準的な量子論理(直交加群格子)を修正し、ある命題が真でありかつ偽でもあるという状況を許容します。
この論理体系では、量子状態が性質を同時に確証しつつ同時に否定するような場面を表現できます。量子力学の操作的形式において、量子パラドックスが体系全体を矛盾に陥れることなく扱える点が重要です。
ダ・コスタとデ・ロンドの革新的アプローチ
Newton da CostaとChristian de Rondeは、従来の量子重ね合わせ解釈がすべて「矛盾を明示的に認めることを避けている」と批判しました。彼らは矛盾を量子現実の核心と見なし、重ね合わせ状態をパラコンシステント論理で直接記述することを提案しました。
このアプローチでは、量子系の記述において矛盾を回避しようとするのではなく、矛盾を本質的な特徴として積極的に取り入れます。これにより、測定問題や波動関数の崩壊といった概念的困難に対して、新しい解釈的視点が開かれる可能性があります。
ブラジル学派の理論的貢献
ブラジルのパラコンシステント論理研究グループは、この分野で重要な役割を果たしています。Carnielliが開発した「形式的不整合の論理(LFIs)」は、矛盾の程度を制御しながら推論を進める枠組みを提供します。またKrauseの準集合論は、量子粒子の非個別性を扱う新しい数学的基礎を提示しています。
これらの理論は、量子物理学の基礎論だけでなく、AI推論システムの設計にも影響を与えています。
AI・機械学習への応用可能性
不整合データを扱う知識システム
現実世界のデータベースや知識グラフは、しばしば矛盾を含みます。複数の情報源を統合する際、相反する情報が共存することは珍しくありません。古典論理に基づくAIシステムでは、こうした矛盾が爆発原理により推論の破綻を招く可能性があります。
パラコンシステント論理は、矛盾を局所化し、推論を継続可能にします。具体的な応用例として以下が挙げられます:
- データベース統合:異なる組織のデータベースをマージする際、矛盾した情報を排除せずに保持しながら有用な推論を行う
- オントロジーマージ:複数の知識オントロジーを統合する際、概念定義の不一致を許容しながら意味的推論を維持する
- 知識グラフの矛盾処理:大規模知識グラフにおける矛盾を検出し、それでも有用なクエリ応答を提供する
Carnielliらの形式的不整合の論理(LFIs)は、こうしたAI応用において特に影響力を持っています。
ニューラルネットワークとの統合
近年、パラコンシステント論理をニューラルネットワークアーキテクチャに統合する研究が進んでいます。従来のニューラルネットは、矛盾した証拠が入力された場合、それらを単純に平均化するか、より強い証拠を優先する傾向があります。
しかしパラコンシステント論理を活用することで、矛盾した証拠を無視せず、整合的に保持したまま扱うモデルが設計できる可能性があります。これは特に以下の分野で有望です:
- 説明可能AI(XAI):モデルの予測に対する複数の説明が矛盾する場合、四値論理(真・偽・両方・どちらでもない)を用いて説明の整合性を管理する
- マルチエージェントシステム:異なるエージェントが矛盾した情報を持つ場合でも、協調的推論を実現する
- 不確実性のある医療診断:複数の診断結果が矛盾する場合でも、すべての証拠を考慮した総合的判断を支援する
量子認知モデルとAI推論
人間の認知や意思決定は、しばしば古典確率の法則に従わないことが知られています。結合錯誤や文脈効果といった現象は、量子確率モデルでよりよく説明できることが実証されています。
Busemeyer、Trueblood、Pothosらの研究グループは、量子確率を認知科学に導入し、AI推論の新しい基盤として位置づけています。このアプローチでは:
- 概念を重ね合わせ状態として表現する
- 文脈依存的な推論をモデル化する
- 人間に近い非古典的推論パターンを実現する
こうした量子認知モデルは、自然言語理解や意思決定支援システムにおいて、より人間的なAI推論を実現する可能性を秘めています。
量子計算による論理推論の高速化
量子コンピュータは、重ね合わせや非可換操作を自然に処理できるため、パラコンシステント推論との親和性が高いと考えられています。現在、以下のような研究が進行中です:
- 論理推論の量子アルゴリズム:古典計算では指数時間を要する推論問題を、量子アルゴリズムで多項式時間に削減する
- 量子機械学習:量子状態を特徴空間として利用し、古典的には困難なパターン認識を実現する
- 量子知識グラフ:量子状態の重ね合わせを利用して、複数の可能性を並列的に探索する
IBMの「Embed2Reason」プロジェクトや、MIT・Oxfordなどの研究機関で量子コンピュータによる論理推論(Quantum Reasoning)の実用化が探求されています。
ハイブリッド推論モデルの構築
量子論理格子を用いたAIフレームワーク
論理構造と物理構造を統合する試みとして、決定構造に量子論理格子を用い、推論エンジンにパラコンシステント論理を採用するAIフレームワークが提案されています。このハイブリッドアプローチでは:
- 知識表現に量子的重ね合わせの概念を導入し、確定していない情報や曖昧な概念を自然に扱う
- 推論プロセスでパラコンシステント論理を用いることで、矛盾耐性を持つ
- 意思決定において量子格子的構造を活用し、複数の可能性を同時に評価する
AGI(汎用人工知能)アーキテクチャの概念モデルでは、こうした矛盾許容論理と量子的構造の統合が、人間レベルの柔軟な推論に不可欠である可能性が指摘されています。
量子的知識埋め込み
Gargらの「Quantum Embedding of Knowledge」研究では、論理知識をヒルベルト空間に埋め込み、論理関係を幾何学的関係として扱います:
- 命題をベクトルや部分空間として表現する
- 論理積は部分空間の交わり、論理和は生成部分空間に対応する
- 射影演算により、関連する概念間の類似度を測定する
このアプローチにより、重なった概念や矛盾した性質を滑らかに扱える知識表現が可能になります。自然言語処理における単語埋め込みの量子版として、より豊かな意味表現が期待されています。
非古典的集合論・圏論による基礎づけ
より根本的なレベルでは、矛盾許容集合論や量子内部論理を持つ圏論的枠組みが研究されています。これらは:
- 量子測定問題に対する新しい数学的視点を提供する
- 非局所性や文脈性といった量子的特徴の形式的扱いを改善する
- AI推論システムの数学的基礎を再構築する可能性を示唆する
こうした基礎研究は、短期的な応用よりも、長期的な理論的革新につながる可能性があります。
主要な研究者と研究動向
パラコンシステント論理の開拓者たち
この分野の発展には、複数の先駆的研究者の貢献があります:
**Newton da Costa(ブラジル)**は、パラコンシステント論理の創始者として、量子重ね合わせを矛盾として扱う新しい解釈を提案し、多くの後続研究に影響を与えました。
**Stanisław Jaśkowski(ポーランド)**は、爆発原理を避ける最初期の矛盾許容論理を構築した人物として知られています。
**Graham Priest(英国・豪州)**は、「真の矛盾が存在する」とするディアレテイズムを擁護する代表的哲学者で、量子力学における矛盾の可能性を論じています。
量子論理の形式化を進めた研究者
**Dalla ChiaraとGiuntini(イタリア)**は、パラコンシステント量子論理の創始者として、量子論理全般の形式化に大きな影響を与えました。
**Mittelstaedt(ドイツ)**は、非古典論理を量子基礎論へ導入する研究の中心人物として活躍しました。
現代の応用研究グループ
ブラジルのパラコンシステント論理研究グループは、Carnielliの形式的不整合の論理(LFIs)やKrauseの準集合論を通じて、量子物理学とAIへの応用を深めています。
量子認知とAIの分野では、BusemeyerTrueblood、Pothosらが量子確率モデルを認知科学に導入し、AI推論の新しい基盤として位置づける研究を進めています。
産業界では、IBMやMIT、Oxfordなどの機関で量子コンピュータによる論理推論の実用化研究が進行中です。
今後の展望と課題
パラコンシステント論理と量子力学の融合は、理論的にも応用的にも大きな可能性を秘めています。古典論理の制約を超えた推論システムは、矛盾や曖昧性を含む現実世界の問題により効果的に対処できる可能性があります。
しかし同時に、いくつかの課題も存在します:
計算複雑性の問題として、パラコンシステント推論は古典論理よりも計算コストが高くなる傾向があります。実用的なシステムでは、推論の効率性と表現力のバランスが重要になります。
解釈の問題として、パラコンシステント論理で「真かつ偽」とされる命題が、現実世界で何を意味するのかという哲学的問いは依然として議論が続いています。
また、量子計算の実用化には技術的ハードルが残されており、理論的可能性が実際のシステムとして実現されるまでには時間を要する可能性があります。
それでも、矛盾を含みながらも破綻しない推論体系、量子的重ね合わせを活用した知識表現、文脈依存的で柔軟な意思決定システムといった方向性は、次世代AIの重要な研究テーマとして注目に値します。
まとめ:非古典論理が拓く新しいAIの可能性
パラコンシステント論理と量子力学は、古典的な二値論理の枠組みを超えて、より柔軟で現実に即した推論体系を提示しています。両者に共通する特徴—真と偽の共存、非可換的・文脈依存的構造、排中律や矛盾律の破れ—は、現実世界の複雑さをより適切に捉える理論的基盤となります。
AI・機械学習への応用においては、不整合データの処理、矛盾を含む知識グラフの推論、人間に近い非古典的認知のモデル化など、多様な可能性が開かれています。量子計算との組み合わせにより、さらに強力な推論システムが実現される可能性もあります。
この分野の研究は、量子物理学の概念的理解を深めるだけでなく、矛盾や曖昧性を含む複雑な現実世界と対峙する、ロバストで柔軟な次世代AI設計に大きく寄与する可能性を秘めています。今後の理論的発展と実用化の進展が期待されます。
コメント