はじめに:量子技術の発展を支える幾何学と測定理論
量子コンピュータや量子センサーの実用化が近づく中、量子状態を正確に理解し制御する技術の重要性が高まっています。本記事では、量子情報科学の基盤となる二つの重要な研究領域——量子情報幾何学におけるリッチ曲率テンソルの計算と量子トモグラフィのリアルタイム測定技術——について、最新の理論的展開を紹介します。
これらの技術は、量子状態空間の幾何学的特性を解明し、効率的な状態推定を実現することで、量子デバイスの性能向上やエラー補正の精度改善に貢献する可能性を秘めています。
量子情報幾何学とは:状態空間を曲率で理解する
量子状態空間の幾何学的アプローチ
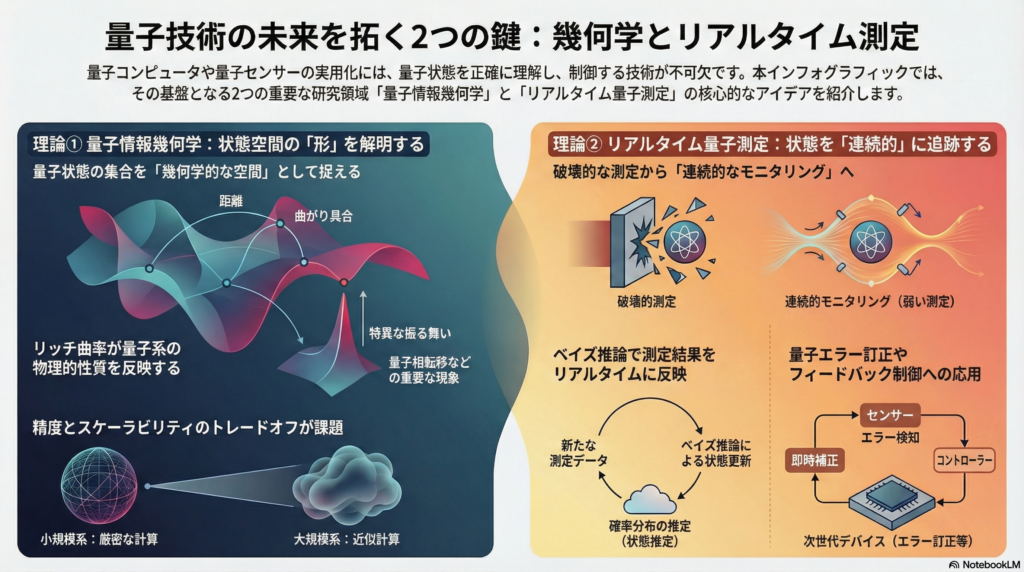
量子情報幾何学は、量子状態の集合を幾何学的な空間として捉え、その性質を調べる分野です。古典的な統計学における情報幾何学の量子版とも言え、密度行列で表される量子状態の間に「距離」や「角度」といった幾何学的概念を導入します。
この幾何学的視点により、量子状態間の類似性や、パラメータ推定における最適性などを統一的に理解できるようになります。特に重要なのが量子計量と呼ばれる概念で、量子状態空間に定義されるリーマン計量の一種です。
代表的な量子計量の特徴
量子状態空間には複数の計量が定義できますが、特に重要なものとして以下が挙げられます:
Bures計量(量子フィッシャー情報計量) 混合状態を含む量子状態空間で広く用いられる計量で、量子統計における推定精度の理論的限界を与えます。この計量は量子フィッシャー情報に基づいており、パラメータ推定において達成可能な最高精度(量子クラメール・ラオ下界)と直接関係します。モノトニー性という重要な性質を持ち、物理的な操作(完全正値写像)によって減少しないという特徴があります。
Fubini-Study計量 純粋状態のみを考える場合に用いられる標準的な計量です。複素射影空間上の自然な計量であり、量子力学における幾何位相(Berry位相)とも深く関連しています。特に2準位系の純粋状態空間は球面と同じ構造を持ち、一定の正の曲率を持つことが知られています。
リッチ曲率テンソルの計算手法:理論と実践のバランス
リッチ曲率が明らかにする量子系の性質
リッチ曲率テンソルは、リーマン幾何学における基本的な概念で、空間の曲がり具合を表します。量子情報幾何学において、リッチ曲率は単なる数学的対象ではなく、量子系の物理的性質を反映する重要な指標となります。
例えば、量子相転移が起こる点では量子フィッシャー情報計量の曲率に特異な振る舞いが現れることが報告されています。また、パラメータ推定の難しさや量子状態の複雑さとも関連があり、情報幾何学的な視点から量子系を評価する新たな手法として注目されています。
効率的な計算アプローチ
リッチ曲率テンソルを実際に計算するには、計量テンソルからクリストッフェル記号、リーマン曲率テンソルと順に求め、最終的に縮約する必要があります。しかし量子系では状態空間の次元が系のサイズに応じて指数関数的に増大するため、全空間での厳密計算は極めて困難です。
そこで現実的には以下のような戦略が取られます:
対称性を活用した解析的手法 系の持つ対称性を利用して計算を簡略化します。特に低次元系や高対称性を持つ系では、Bures計量に対する解析的な公式が導出されています。例えば1量子ビット系では比較的単純な曲率構造を持つことが知られていますが、次元が上がると複雑化し、一般には一定曲率や局所対称性を持たないことが明らかになっています。
数値計算による近似 高次元系では数値的手法で近似計算を行います。パラメータ空間をサンプリングし、有限差分などで曲率を評価する方法です。計算コストは高いものの、現代の計算機性能であれば小規模系では実現可能です。
部分空間への制限 全状態空間ではなく、物理的に重要な部分空間(例:ガウス状態、コヒーレント状態など特定のパラメータで記述できる状態族)に限定することで、計算を大幅に簡略化できます。この手法は実用上の問題に焦点を当てる場合に有効です。
精度とスケーラビリティのトレードオフ
リッチ曲率計算において、数学的精度と計算効率・スケーラビリティは常にトレードオフの関係にあります。厳密な解析解は小規模かつ対称性の高い系に限られ、より現実的な大規模系では近似や数値計算に頼らざるを得ません。
特に混合状態空間では、純粋状態に近づく極限で計量が発散する場合があり、全空間を一様に扱うことが理論的にも困難です。このため、目的や系の規模に応じて適切な計算手法を選択することが重要となります。
量子トモグラフィ:未知の量子状態を測定から再構成する
量子トモグラフィの基本原理
量子状態トモグラフィは、未知の量子状態を測定データから推定・再構成する技術です。医療のCTスキャンに似た原理で、様々な角度から「測定」を行い、その結果を統合して全体像を復元します。
基本的な手順は以下の通りです:
- 同一の量子状態を多数準備
- 異なる基底や可観測量で測定を実施
- 得られた統計データから密度行列を推定
単一量子ビットの場合、X、Y、Z軸方向での測定結果から状態を完全に決定できます。しかし問題は系のサイズが大きくなった場合です。
スケーラビリティの課題と解決策
量子トモグラフィの最大の課題は、必要な測定数が系のサイズに対して指数関数的に増大することです。n量子ビット系では密度行列が2^n × 2^n のサイズとなり、完全な状態決定には膨大な測定が必要となります。
この問題に対して、近年様々な効率化手法が提案されています:
圧縮センシング量子トモグラフィ 実際の量子状態が低ランク(純粋状態に近い)であることを利用し、必要測定数を劇的に削減する手法です。ランダム測定と凸最適化を組み合わせることで、従来手法の数分の一以下の測定で状態推定が可能になる場合があります。
古典的シャドウ法 ランダムに選んだ基底で少数回の測定を繰り返し、状態の「影絵」を得る新しいアプローチです。完全な状態ではなく、特定の物理量の期待値を効率的に推定できます。
機械学習による推定 ニューラルネットワークなどを用いて、測定データから直接密度行列を予測する手法も研究されています。
これらはいずれも、完全な精度と実用的な測定数のバランスを取るアプローチと言えます。
リアルタイム測定技術:量子状態を連続的にモニタリングする
連続測定モデルの革新性
従来の量子トモグラフィは、多数の同一状態を破壊的に測定してデータを集めるバッチ処理型でした。これに対しリアルタイム量子測定は、測定結果が得られるごとに逐次的に状態推定を更新し、常に最新の推定値を得る新しいパラダイムです。
この実現の鍵となるのが連続弱測定です。系を一度に投影破壊するのではなく、弱い相互作用を通じて連続的に観測します。一回の測定で得られる情報は微小ですが、系への擾乱も小さいため、同じ系から時間をかけて情報を取り出せます。
さらに、測定と並行して系に制御ハミルトニアンを印加することで、観測可能量を動的に変化させ、様々な情報を効率的に抽出できます。この手法により、従来は別々の測定で得ていた情報を単一の連続測定系列で取得することが可能になります。
ベイズ推論による状態推定
連続測定から得られるデータをリアルタイムで処理するには、ベイズフィルタリングが用いられます。これは古典的なカルマンフィルタの量子版とも言える手法で、以下のプロセスを繰り返します:
- 現在の状態推定を事前分布とする
- 新たな測定結果を取得
- ベイズの定理で事後分布に更新
- 次のステップの事前分布とする
重要なのは、この更新が測定による擾乱を織り込んでいることです。量子力学では測定が系に影響を与えるため、単なるデータ同化ではなく、測定理論と整合した推定法となっています。
このアプローチにより、時間とともに変化する量子状態をリアルタイムで追跡できるだけでなく、測定で得た情報を即座にフィードバック制御に利用することも可能になります。
実験実証と応用例
リアルタイム量子測定技術は、既にいくつかの実験で実証されています。原子スピン系での実験では、セシウム原子集団のスピン状態を弱測定しつつ制御を加えることで、様々な未知初期状態を短時間で再構成することに成功しており、推定精度(忠実度)は約90%に達しています。
理論的には、2量子ビット系において1量子ビットのみを測定しながら両方の状態を推定する手法も提案されており、シミュレーションでは忠実度0.98以上の再構成が報告されています。
この技術の応用先として期待されるのは:
- 量子エラー補正:連続モニタリングでエラーを早期検知し即座に補正
- 量子フィードバック制御:推定結果に基づいて即座に制御を調整
- 適応的量子センシング:リアルタイム推定で測定設定を最適化
特に量子コンピュータのエラー補正において、従来の離散的補正ではなく連続的にエラーを監視・補正する戦略は、次世代デバイスでの重要な方向性となっています。
最新研究動向:理論と応用の融合
情報幾何学の新展開
量子情報幾何学は、量子多体系や場の理論への応用が進んでいます。量子相転移の指標として量子フィッシャー計量の発散やリッチ曲率の特異性を利用する研究、多パラメータ同時推定における曲率の役割を調べる研究などが活発です。
興味深いのは、量子機械学習への応用です。変分量子回路のパラメータ空間に量子フィッシャー計量を導入し、その曲率が学習の汎化性能や勾配消失問題に関係することが示唆されています。情報幾何学的視点が、量子アルゴリズムの設計指針を提供する可能性があります。
トモグラフィの効率化と実時間化
量子トモグラフィの分野では、効率化とリアルタイム化が二大テーマとなっています。適応型トモグラフィ(測定結果に応じて次の測定を選ぶ)、機械学習によるノイズ除去など、限られたリソースで高精度推定を実現する工夫が続いています。
リアルタイム化では、量子フィードバック制御との統合が注目されています。測定が「結果を知る」ためだけでなく「結果を利用して次のアクションを起こす」段階に入り、オンライン校正・補正・最適化が現実のものとなりつつあります。
精度・効率・スケーラビリティの三角関係
これらの研究に共通するのは、数学的精度、計算効率、スケーラビリティという三つの要素のバランスを取る必要性です。
厳密な理論計算は小規模系に限られ、大規模系では近似が不可欠です。リアルタイム処理では計算時間の制約があり、モンテカルロ近似や縮約モデルなど、精度を犠牲にする代わりに実用性を重視する選択も必要です。
目的に応じてこのトレードオフをどう設定するか——例えば「一度きりの高精度測定」より「常時監視する中程度精度測定」が有利な場合もある——が、実用化における重要な設計判断となります。
まとめ:量子技術の未来を拓く基礎理論
量子情報幾何学におけるリッチ曲率テンソルの研究と、量子トモグラフィのリアルタイム測定技術は、一見異なる分野に見えますが、いずれも「量子状態空間をいかに効率的に理解・測定するか」という共通の課題に取り組んでいます。
幾何学的視点は量子系の深い性質を明らかにし、最適な推定戦略や制御手法の設計指針を提供します。一方、リアルタイム測定技術は、その理論を実際の量子デバイスで活用する道を開きます。
量子コンピュータや量子センサーの実用化が進む中、これらの基礎理論の重要性はますます高まるでしょう。精度と効率のバランスを取りながら、理論研究と技術開発の相乗効果によって、量子技術は新たな段階へと進化していくと期待されます。
コメント