量子認知モデルとは:言語モデル評価への新しいアプローチ
近年、大規模言語モデル(LLM)の性能評価において、従来の古典的確率論では捉えきれない現象が注目を集めています。そこで登場したのが量子認知モデル(Quantum Cognition)です。このアプローチは、確率の重ね合わせや干渉効果といった量子力学の概念を借りて、人間の意思決定や認知における非古典的な現象を説明する枠組みです。
言語モデルの振る舞いを量子認知的に分析することで、文脈依存的な判断や矛盾した選好といった、頻度主義的アプローチでは説明困難だった性質を浮き彫りにできる可能性があります。本記事では、言語モデルに対する量子認知モデルの適用事例、干渉効果の測定方法、そしてKLダイバージェンスを中心とした評価指標について詳しく解説します。
言語モデルにおける量子認知アプローチの実証研究
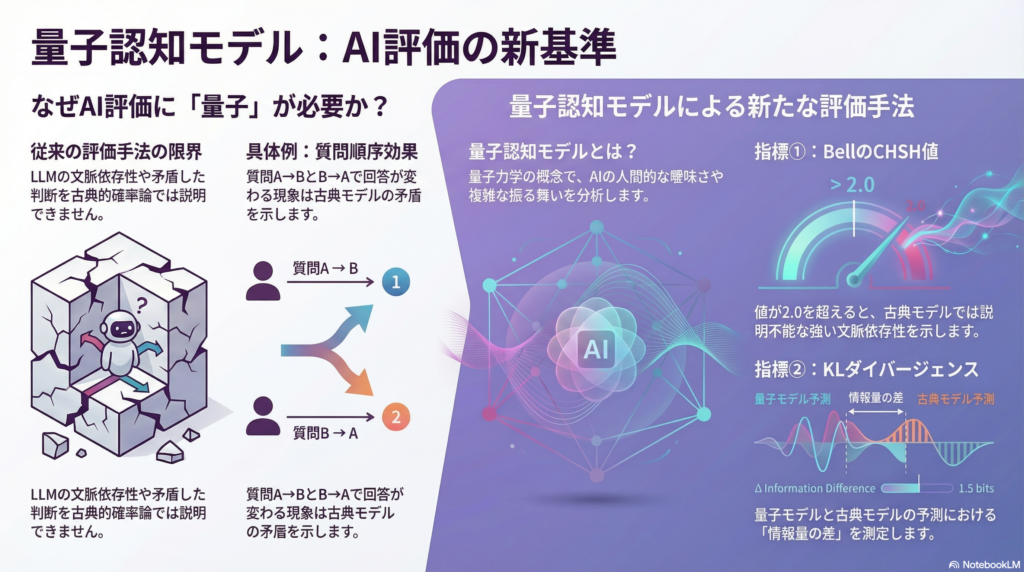
LLMの非古典的な文脈依存性を検証する
Agostinoら(2025)は、LLMを「認知システム」として扱い、曖昧な単語対に対する解釈を量子的文脈性の観点から評価しました。彼らは意味論的ベル不等式テストをLLMに適用し、CHSH値(BellのCHSH測度)を算出しています。
実験の結果、CHSH値が平均1.2〜2.8、特に2.3〜2.4といった値を示すケースが確認されました。これは古典的上限である2を明確に超える値であり、曖昧な言語解釈において古典的確率論では説明できない文脈依存性が現れることを示唆しています。この結果は、人間の認知実験で得られていた非古典的効果とも一致しており、言語モデルの意味理解に量子的アプローチを適用する有効性を示しています。
感情分析タスクへの応用
自然言語処理分野では、感情分析などのタスクに量子認知の考え方を取り入れたモデルも登場しています。Liuら(2023)のサーベイによれば、量子確率の形式とディープラーニングを組み合わせた感情分析モデルが提案されており、従来型のモデルと比較して有望な性能を示しているとされています。
量子論的手法は曖昧さや文脈依存性の扱いに強みがあり、感情極性の判断など人間の主観が絡む課題で有効性が報告されています。このように、言語モデル領域でも量子認知に着想を得た手法が台頭しつつあり、その評価には従来と異なる観点が求められています。
干渉効果とは:定義と実験例
干渉効果の基本概念
干渉効果(インターフェレンス効果)とは、ある事象の生起確率が他の事象や文脈の影響で古典的な法則から逸脱する現象を指します。典型的には確率の加法性や全確率の法則が成り立たないパターンとして現れます。量子認知モデルでは、波動的な重ね合わせによってこれを説明します。
人間の意思決定における干渉効果の古典的実験例として、質問順序効果や選択肢提示順序の影響が挙げられます。世論調査で質問AとBを尋ねる順序を入れ替えると回答率が変化するという現象は、古典確率論ではP(A)は固定であるはずなのに順序で変わるという矛盾を示しています。
カテゴリー化と意思決定の干渉
Wangらの研究では、被験者にまず刺激(例:人物の顔)を提示してカテゴリー判断させ、その後に行動選択をさせる二段階課題を実施しました。結果、カテゴリー判断を事前に要求した場合と要求しない場合で、後続の行動選択の確率に体系的な差(干渉効果)が生じ、これは古典的な全確率の法則に違反することが確認されています。
この複雑な干渉効果パターンは、従来のマルコフ過程モデルやシグナル検出理論では説明困難ですが、量子認知モデル(BAEモデル)では心理状態を重ね合わせ状態として表現し、観測(カテゴリー報告)が後続選択の状態をエンタングルさせる仕組みで再現可能であると示されました。
Quantum Question(QQ)等式による検証
WangとBusemeyerらは「Quantum Question(QQ)等式」という量子モデル固有の予測を導入し、複数のアンケート調査データにおいてその予測が統計的に支持されることを示しました。QQ等式の成立(もしくは破れ)は、質問順序効果の有無を厳密に検定する量子的なアプローチといえます。
干渉効果の定量的測定方法:4つの主要指標
1. 古典確率からの逸脱量(干渉項)
干渉効果は、古典的な確率予測値との差分として定量化できます。例えば、「カテゴリー事前なし」での行動確率と「カテゴリー=各条件」での行動確率の加重和との差が干渉効果の大きさになります。違いがゼロであれば古典的法則(全確率の法則)が成立し、非ゼロであれば干渉項の存在を示します。
量子モデルではこの差分に対応する項(振幅の積から生じるクロスターム)がモデルパラメータとして現れ、その値で干渉の方向(ポジティブ/ネガティブ干渉)や強さを説明します。
2. BellのCHSH値:非古典的相関の強さを測る
BellのCHSH値は、本来、空間的に離れた二者間の相関の古典的限界を示すものですが、認知文脈では質問ペアやタスクペア間の文脈依存性を測る指標として応用されます。AgostinoらのLLM実験では、LLMの回答を用いてCHSH値を計算し、2を超える値が得られるかをチェックしました。
結果として2.3などの値が観測され、これは古典モデルでは説明不能な強い文脈的相関(すなわち干渉効果)を示す定量的エビデンスとなっています。CHSH値が2を上回ることは、人間の認知実験でも報告されており、量子モデルの予測と一致します。
3. KLダイバージェンス:モデル間の情報量差を測定
Kullback–Leiblerダイバージェンス(相対エントロピー)は、2つの確率分布間の差異を測る一般的な指標です。モデル評価では「データが従う分布」と「モデルが与える分布」間のKLダイバージェンスを算出し、モデルの適合度(情報ロスの少なさ)を測定します。
量子認知モデルの評価でもKLダイバージェンスが活用されており、古典モデルとの出力分布の差異を定量化する手段として用いられます。例えばTuumalaら(2025)は、量子的な干渉項を組み込んだ分類器モデルについて、干渉なし版(古典的合成ルール)との出力確率分布のKL距離を算出し、これを「干渉情報量(Interference Information, J_int)」と定義しました。
J_intが大きいほど量子的干渉が分布に与える影響が大きいことを意味し、モデル間の情報量ギャップとして干渉効果を数値化しています。KLダイバージェンスは0以上の指標で、0なら分布が同一、値が大きいほど乖離が大きいことを示します。
なお、KLは非対称指標であるため、必要に応じて対称化したJensen–Shannonダイバージェンスを使うこともあります。JSDは0〜1に正規化された距離指標で、直感的な解釈がしやすい利点があります。
4. 対数尤度:モデル適合度の直接評価
モデル比較の文脈では、与えられたデータに対する各モデルの尤度(またはその対数値)を算出し、その差分で優劣を評価する方法も取られます。対数尤度の差は、モデルの当てはまりの良さの差であり、統計的にはそれに基づいて情報量基準(AICやBIC)を算出したり、Vuong検定(非入れ子モデルの尤度比検定)を行ったりすることも可能です。
量子モデルと古典モデルの比較では、データにフィットさせた際の対数尤度を比較し、どちらがデータ生成過程に近いかを評価します。このアプローチはKLダイバージェンスとも深く関係しており、ある真の分布に対してモデルの予測分布のKLダイバージェンスを最小化することが対数尤度の最大化に相当します。
KLダイバージェンスによる量子モデルと古典モデルの比較事例
二段階ギャンブルにおける非合理選好の分析
Broekaertら(2020)は、TverskyとShafir(1992)が報告したディスジャンクション効果(確実性の原理の違反)をオンライン実験で再調査し、参加者データを3種類のモデルで説明できるか比較しました。
比較されたモデルは以下の通りです:
- ヒューリスティックなロジスティックモデル:経験則的な決定ルールをロジスティック回帰で表現し、文脈や直前の結果の影響をパラメータに含めたモデル
- マルコフ過程モデル(古典確率モデル):古典的な状態遷移に基づくモデルで、直前のギャンブル結果に応じて選好が変化するが線形効用や文脈効果を組み入れた拡張版
- 量子確率モデル(量子ダイナミクスモデル):上記マルコフモデルに形を合わせつつ、状態をヒルベルト空間上で記述し、干渉項に相当する動的な文脈効果を含んだモデル
比較の結果、ロジスティックモデルや線形効用に基づくマルコフモデルでは実験で観察された確率パターン(順序効果や選好のインフレ/デフレ効果)を統一的に説明できないことが判明しました。一方で、量子ダイナミクスモデルは観測データ中の主要な効果を全て定性的にも定量的にも説明可能であり、データへの適合度でも他モデルを上回りました。
質問順序効果における検証
質問順序効果に関するWang & Busemeyer(2013)の研究でも、量子モデル(QQモデル)が経験的に観察される制約式(QQ等式)を満たす一方、従来モデルでは説明できないことが示されています。さらに、感情分析タスクにおける量子インスパイアモデルの研究では、精度やF値といった従来指標でも古典的ディープラーニングモデルに匹敵するかそれ以上の性能が報告され、特に不確実性の定量化や文脈の動的反映において量子モデルが優位であったとされています。
これらの結果から、KLダイバージェンスや対数尤度といった統計的指標の観点でも、量子認知モデルがヒューリスティックモデルや従来確率モデルより良好な適合を示すケースが複数確認されています。
ヒューリスティックモデルとの統合的評価枠組み
ヒューリスティックモデルの特徴と限界
ヒューリスティックモデルとは、人間が用いる単純な意思決定ルールや近似的な推論法則をモデル化したものです。代表的な例として代表性ヒューリスティックや利用可能性ヒューリスティックなどがあり、従来の心理学ではこれらが人間の非合理な判断の原因とされてきました。
量子情報アーキテクチャによる統合アプローチ
Kvamら(2015)は、ヒューリスティックが暗黙に仮定している古典論理構造に注目し、それを量子論理に置き換える「量子情報アーキテクチャ」を提案しました。彼らによれば、古典論理に基づくヒューリスティックはしばしば経験的データと食い違う予測を出すが、それはルール自体というより古典的前提によるものであると指摘しています。
ヒューリスティックの処理手続きをそのままに、根底の論理を量子論理(非可換な射影測定の枠組み)に置き換えると、従来の矛盾が解消されデータに近い予測が得られることを示しました。例えば認知的プロセスを量子回路的に記述し、各ステップ(キューのチェックや閾値判断)に量子的な停止規則を組み込むことで、fast-and-frugal(速くて粗削り)ヒューリスティックがより柔軟で記述的妥当性の高いモデルに拡張できると述べています。
統合による双方向のメリット
この統合的枠組みでは、ヒューリスティックモデルが得意とする計算効率や解釈の明快さと、量子モデルの記述力(データ適合の良さ)を両立できる可能性があります。実際、「量子論理への置換によりヒューリスティックモデルの予測精度が向上し、量子モデル側も心理学的プロセスの観点から具体化される」という双方向のメリットが指摘されています。
評価における理論的課題と今後の展望
モデル複雑性とパラメータ数の問題
モデル比較の際には、パラメータ数の差にも注意が必要です。複雑なモデルが単に自由度の多さでデータに適合していないかを確認するために、情報量規準(AICやBIC)を用いることが一般的です。
理論的課題としては、量子認知モデルが示す非古典的効果をどの程度まで古典モデルで近似再現できてしまうかという問題があります。例えば、古典モデル側に新たな階層や文脈依存パラメータを加えれば干渉効果を擬似的に再現できる可能性もあり、その場合に量子モデルを採用する意義が問われます。
この点について、量子モデルはパラメータを増やすことなく原理的に干渉項を内包できること、複数の現象を統一的メカニズムで説明できることが利点とされています。
LLMの多段対話への適用
今後の課題として、より複雑な言語モデルの振る舞い(例:LLMの多段対話における文脈効果)に対して量子認知モデルがどこまで有効か検証し、評価指標としても人間の直感に一致する新たなメトリクスを開発していく必要があるでしょう。
加えて、計算コストの問題やモデル解釈性の確保も無視できず、ヒューリスティックな簡便さと量子的精密さを両立するアプローチが模索されています。
まとめ:量子認知モデルが拓く言語モデル評価の新地平
量子認知モデルを言語モデル評価に適用する取り組みは、曖昧性や文脈による影響を定量的に評価する新たな視点を提供します。干渉効果の検出と測定においては、従来の古典モデルでは見逃されがちな確率の微妙な揺らぎや相関を浮き彫りにし、CHSH値やKLダイバージェンスといった指標によってその非古典性を検証できます。
特にKLダイバージェンスは、モデル予測分布と実データ分布あるいは古典モデル分布との間の情報量ギャップを示すことで、量子モデルの優位性を示すエビデンスとなります。さらに、ヒューリスティックモデルとの比較評価では、単なる精度比較だけでなく人間の認知的特徴を捉えたモデルかどうかという質的評価も重要です。
評価枠組み自体の革新も重要なポイントです。量子認知的アプローチは、新しい実験パラダイム(例えば心理学的ベルテスト)や新指標の導入によって、言語モデルやAIシステムの理解に貢献しつつあります。これは、人間の言語理解や意思決定のダイナミクスを模倣・評価する上で極めて興味深い方向性であり、従来の枠組みに量子的発想を取り入れることで見落とされていた現象を発見・定量化できることを示しています。
コメント