ホログラフィック原理が示す時空の新しい見方
現代物理学における最も革新的な洞察の一つが、時空と量子情報の深い結びつきです。ホログラフィック原理は「空間の内部で起こる物理現象は、その境界面上の情報だけで完全に記述できる」という驚くべき主張を提示しています。この原理は、ブラックホールのエントロピーが事象の地平面の面積に比例するというベケンシュタインの発見から着想を得たもので、情報が体積ではなく面積に比例して格納されることを示唆しています。
本記事では、ホログラフィック原理の具体的実現であるAdS/CFT対応を中心に、量子情報理論がいかに時空の理解を深めているかを探ります。エンタングルメントと幾何学の関係、量子誤り訂正符号による新しい解釈、そして「時空が量子情報から創発する」という最新の研究動向まで、体系的に解説していきます。
AdS/CFT対応:重力理論と量子場理論の等価性
AdS/CFT対応は、Juan Maldacenaが1997年に提唱した画期的な理論的枠組みです。この対応は、(d+1)次元の反ド・ジッター空間(AdS)上の重力理論と、d次元の共形場理論(CFT)が数学的に等価であることを主張します。
ホログラフィー双対の基本構造
最も研究されている例では、5次元AdS空間上のタイプIIB超重力理論が、4次元のN=4スーパーYang-Mills理論の大きなN極限に対応します。ここで重要なのは、AdS空間の「バルク」(内部)における重力現象が、その「境界」に位置するCFTの量子状態として完全に記述できるという点です。
この対応関係において、境界上の量子論の各状態・演算子は、バルク内部の重力理論における対応物と一対一に結びつけられます。言い換えれば、境界上の量子情報がバルクの時空構造そのものを描き出すという構図が成立しています。
理論物理学への多面的影響
AdS/CFT対応は当初、超弦理論の文脈で登場しましたが、その応用範囲は予想をはるかに超えて広がりました。量子重力の非摂動的定義を与える可能性を秘めているだけでなく、強相関量子多体系の解析ツールとしても有用性が認められています。特に近年は、量子情報理論の言葉でこの対応を再解釈する試みが活発化しており、時空の本質に迫る新たな視点を提供しています。
エンタングルメント・エントロピーと時空幾何の深い関係
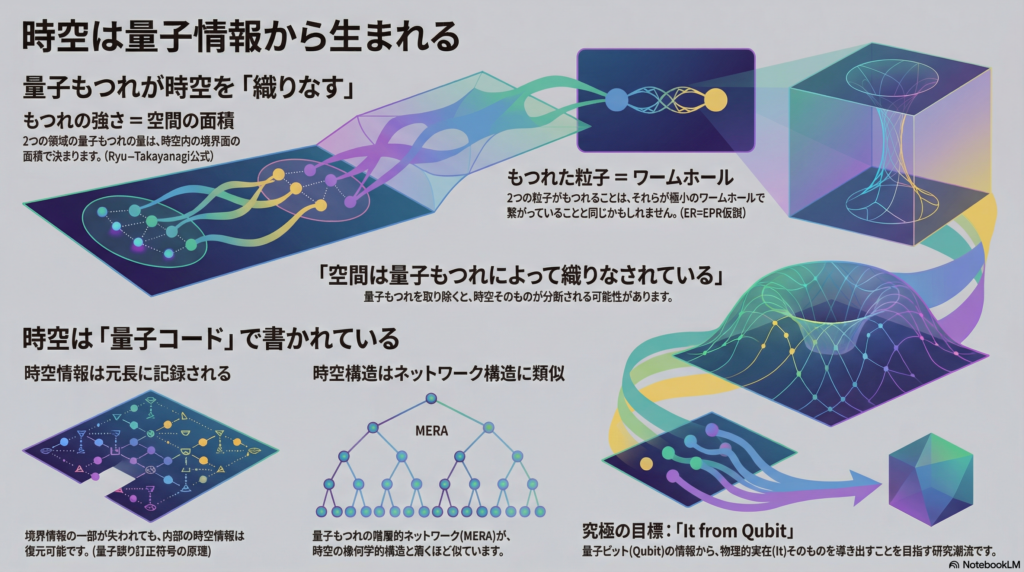
量子もつれ(エンタングルメント)は、ホログラフィーにおいて時空構造と本質的に結びついています。この関係を定量的に表現するのが、Ryu–Takayanagi公式です。
Ryu–Takayanagi公式の革新性
2006年にShinsei Ryuと高柳匡が提案したこの公式は、境界CFTのある領域におけるエンタングルメント・エントロピーが、バルクAdS空間内の極小曲面の面積によって与えられることを示しています。具体的には、境界上の領域Aのエントロピーは、その領域に対応するバルク内の極小曲面γ_Aの面積に比例し、S_A = Area(γ_A)/(4G_N)という形で表されます。
この公式はブラックホールのベケンシュタイン–ホーキングの面積–エントロピー関係と構造的に類似しており、量子もつれという純粋に量子情報的な概念と、時空の幾何学的性質を直接結びつける画期的な成果となりました。
エンタングルメントが織りなす時空
Mark Van Raamsdonkは2010年の研究で、古典的に連結な時空が存在するためには、その根底に量子的エンタングルメントが必要であると主張しました。彼の議論によれば、時空中の二つの領域からエンタングルメントを取り除くことができれば、その領域同士の繋がりは引き裂かれ、時空が分断される可能性があります。
この洞察は「空間は量子もつれによって織りなされている」という直観的な描像を与え、エンタングルメントが時空の位相や幾何を根本的に決定づけるという考え方を支持しています。
エンタングルメント熱力学と重力方程式
さらに注目すべき成果として、Lashkariらによる2013年の研究があります。彼らは、エンタングルメント・エントロピーの変化とエネルギー変化の関係(エンタングルメント熱力学第1法則)を境界理論で課すと、ホログラフィー的にはバルクのアインシュタイン方程式の線形摂動形が導かれることを示しました。
この結果は、量子もつれの物理法則が重力の場の方程式を生み出すことを意味しており、エンタングルメントと時空幾何の等価性を強く支持する証拠となっています。時空の動力学そのものが、量子情報の法則から創発する可能性を示唆しているのです。
ER=EPR仮説:量子もつれとワームホールの同一視
ER=EPR仮説は、2013年にJuan MaldacenaとLeonard Susskindが提唱した大胆な仮説で、量子もつれ(EPR相関)と時空のワームホール(Einstein-Rosenブリッジ)が本質的に同一の現象の異なる側面であるという主張です。
仮説の核心的主張
この仮説によれば、完全にエンタングルした2つの粒子(EPR対)は、極微視的なワームホールで繋がっていると解釈できます。特にブラックホール物理においては、最大エンタングルした2つのブラックホールが非遍歴的なワームホールで内部が繋がっている(ただし情報伝達はできない)と考えられます。
より極端には、最も単純な2スピンのEPR対ですら、量子的なワームホールで結ばれているかもしれないという可能性が示唆されています。
時空の量子的起源への示唆
ER=EPR仮説は依然として推測的な段階にあり、直接的な検証は困難です。しかし、この考え方は「もつれが時空を織りなす」というホログラフィック原理の理解を大きく前進させる概念的枠組みを提供しています。エンタングルメントによって時空の橋が形成されるという直感は、量子情報と幾何学の深い結びつきをより鮮明に描き出しています。
量子誤り訂正符号がホログラフィーに投げかけた新たな光
AdS/CFT対応の理解において、量子誤り訂正(QEC)の概念が重要な役割を果たすことが明らかになってきました。
バルクの局所性と量子誤り訂正
2015年、Ahmed Almheiri、Xi Dong、Daniel Harlowらは、AdS/CFTにおけるバルクの局所性が量子誤り訂正符号の原理と密接に関連していることを指摘しました。彼らの研究によれば、バルクの演算子情報を境界の一部(サブリージョン)から再構成できるかという問題は、境界理論が実現する量子誤り訂正符号の性質に対応しています。
つまり、AdS/CFTにおけるバルク情報は境界上に冗長に符号化されており、一部の境界情報が失われても(例えば一部の領域を取り除いても)バルクの情報を復元できる可能性があります。これは量子誤り訂正において、一部の量子ビットがエラーで失われても論理情報を取り戻せる性質と本質的に同じ構造です。
HaPPY符号:ホログラフィーの玩具模型
Fernando Pastawski、Beni Yoshida、Daniel Harlow、John Preskillらは2015年に「ホログラフィック量子誤り訂正符号」(HaPPY符号)と呼ばれる具体的な模型を提案しました。この模型では、双曲空間のタイリング上にテンソルネットワークを配置し、バルクの自由度(論理量子ビット)を境界の自由度(物理量子ビット)に符号化しています。
HaPPY符号は完全テンソルと呼ばれる特殊な構造を用いることで、Ryu–Takayanagi公式や三部相互情報の負値といったAdS/CFTのエンタングルメント特性を正確に再現します。さらに、一つのバルク情報を境界の複数の異なる領域から復元できることが明示的に示されており、ホログラフィーにおける情報の冗長性やバルク情報の安全性を具体的に説明する強力なツールとなっています。
量子情報の幾何化と創発する時空の最前線
近年、「量子情報の幾何化」という広範な視点から、時空が量子情報から創発するメカニズムを解明しようとする研究が急速に進展しています。
MERAと双曲幾何の類比
Brian Swingleは2012年に、量子多体系の基底状態を効率よく表現する階層的テンソルネットワークであるMERA(Multiscale Entanglement Renormalization Ansatz)が、AdS空間の構造と深い類似性を持つことを指摘しました。
MERAにおける階層構造は、AdS空間の径方向(スケール方向)に対応し、量子多体系の繰り込み変換スケールと結びついています。MERAネットワークの幾何学は、AdSの空間断面の双曲幾何と驚くほど類似しており、量子もつれを階層的に組み上げるネットワーク構造が、そのままAdS/CFTの時空構造を模倣しているという洞察が得られました。
この「It from MERA」と呼ばれる考え方は、テンソルネットワークを用いてAdS時空の様々な現象を再現する研究へと発展しています。
量子回路の複雑性と時空の体積
Leonard Susskindらは、ブラックホール内部の体積や作用といった幾何学的量を、境界上の量子状態の回路複雑性に結びつける仮説を提唱しました。「複雑性=体積」や「複雑性=作用」といった対応関係は、エンタングルメントでは捉えきれないブラックホール内部の動的性質を理解する鍵として研究が進められています。
量子回路の複雑性は、ある量子状態を基準状態から準備するために必要な量子ゲートの最小数で測られますが、ホログラフィーではこれが時空中の特定の幾何学的量に対応すると考えられています。この研究方向も、量子情報を幾何学に翻訳する試みの一環と位置づけられます。
It from Qubit:量子情報から実在へ
「It from Qubit(イット・フロム・キュービット)」というスローガンのもと、量子情報(qubit)の構造から時空や重力(It=物理的実在)を理解しようとする研究潮流が形成されています。John Preskillらによって提唱されたこの方向性では、量子エンタングルメント、量子エラー訂正、量子複雑性、量子コヒーレンスといった概念を駆使して、「時空がどのように情報から構築されるのか」を探究する研究が数多く展開されています。
この潮流は、ホログラフィーを超えて量子情報全般を通じて重力理論の基礎を捉え直そうとする野心的な試みであり、量子情報科学と基礎物理学の架け橋として重要な役割を果たしています。
まとめ:時空と量子情報の等価性が開く新しい地平
ホログラフィック原理とAdS/CFT対応は、量子情報理論と深く結びつくことで、時空理解に革新的な視点をもたらしています。エンタングルメントが時空の幾何学そのものを構成し、量子誤り訂正のメカニズムがホログラフィーの情報構造を支え、量子回路の複雑性が時空の動力学的性質を反映するという描像が、徐々に具体的な形を取りつつあります。
Ryu–Takayanagi公式によるエンタングルメントと幾何学の定量的関係、ER=EPR仮説が示唆する量子もつれと時空の橋の同一性、HaPPY符号に代表される量子誤り訂正的解釈、MERAや複雑性研究が示す時空の創発メカニズム――これらすべてが、「時空=量子情報」という等価性を多角的に支持しています。
もちろん、この分野はまだ発展途上にあり、多くの課題が残されています。より一般的な重力理論や現実の宇宙(de Sitter宇宙など)への拡張、時空創発の厳密な定式化、実験的検証の可能性といった問題は、今後の研究を待つところです。しかし、ホログラフィック原理とAdS/CFT対応が切り開いた「量子情報から時空を理解する」という道筋は、21世紀の理論物理学における最も刺激的な研究領域の一つとして、着実に深化を続けています。
コメント