量子力学が古典論理では捉えきれない理由
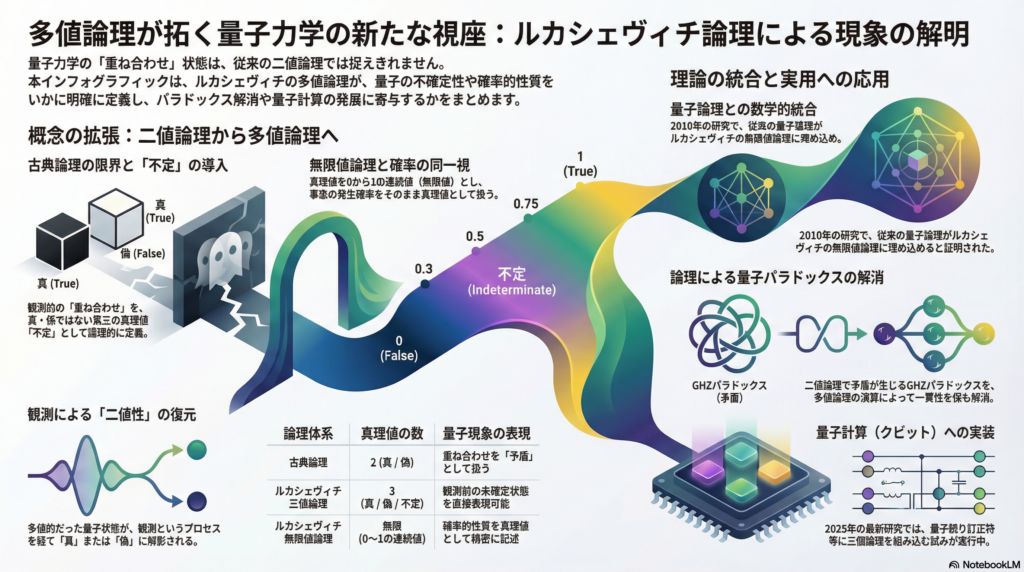
量子力学における粒子の振る舞いは、私たちの日常的な論理感覚とはかけ離れています。シュレーディンガーの猫は「生きている」か「死んでいる」かという二値ではなく、観測されるまで両方の状態が重なり合っている——このような「重ね合わせ状態」を、古典的な二値論理(真または偽)で記述することには限界があります。
この問題に対し、ポーランドの論理学者ヤン・ルカシェヴィチが提唱した多値論理が注目されています。本記事では、量子力学の不確定性と多値論理の関係、特にルカシェヴィチ論理がどのように量子現象の理解に貢献するかを、近年の研究成果とともに解説します。
ルカシェヴィチ三値論理と量子の未確定性
第三の真理値「不定」の導入
ルカシェヴィチは1920年代に、未来の出来事に関する命題には「真」「偽」だけでなく「不定」という第三の真理値を割り当てるべきだと提案しました。この考えは量子力学にも適用可能です。哲学者ハンス・ライヘンバッハは1944年、観測前の量子事象を記述するために三値論理を導入し、測定されるまで決まらない物理量には「不定」の値を与えるべきだと主張しました。
例えば、電子のスピンが測定前に「上向き」か「下向き」か決まっていない状態を、古典論理では矛盾として扱わざるを得ませんが、多値論理では自然に「未確定」という論理的状態として表現できます。
無限値論理と確率的真理値
ルカシェヴィチは後に、真理値が0から1の連続値を取りうる無限値論理へと理論を拡張しました。この枠組みは、量子力学の確率的性質と深く結びつきます。重ね合わせ状態にある量子命題に、0と1の間の実数値(例えば0.3や0.7)を真理値として割り当てることで、量子的な曖昧さを直接表現できるのです。
アンソニー・サドベリーは2017年の研究で、未来の量子事象「Aが起こる」という命題の真理値を、その事象が起こる確率と同一視する時間的多値論理を構築しました。例えば、ある量子過程でAが起こる確率が30%であれば、「Aが将来起こる」という命題の現在の真理値は0.3となります。このアプローチにより、量子の重ね合わせ原理が命題の論理的重ね合わせとして表現され、確率概念に明確な論理的位置づけが与えられました。
観測問題への多値論理的アプローチ
二値性の破れと復元
量子力学の観測問題——観測によって量子状態が突然確定する現象——は、多値論理の観点から新たな解釈が可能になります。観測前の量子系では「真でも偽でもない」中間的な真理値が存在し、観測によって初めて真か偽かに二値化されると考えるのです。
この見方では、観測前には論理的な二値性の原理が破れており、観測によって二値性が復元されることになります。波束の崩壊は、多値だった真理値が二値に射影される過程として理解できます。観測による「飛躍的な変化」も、もともと多値論理の枠組みで記述されていた状態が、測定という物理過程を通じて古典的な二値世界へと移行する自然な過程と捉えられるのです。
多値性から二値性への移行という課題
ただし、アルカディ・ボロティンが2018年の研究で指摘したように、この移行プロセスには理論的課題が残されています。量子レベルでは真理値が多値でも、マクロな観測結果では明確に真偽が定まる——この「二値性の出現問題」をどう整合的に説明するかは、今後さらなる検討が必要な領域です。
量子論理との理論的統合
バーカッフ=フォン・ノイマン量子論理との関係
量子力学の論理的基盤として、バーカッフとフォン・ノイマンが1936年に提唱した量子論理があります。これは射影演算子が成す直交束によって量子命題の構造を記述するもので、分配法則が成り立たない独特の論理体系です。
ヤロスワフ・ピカチュは2010年の画期的な研究で、バーカッフ=フォン・ノイマン型の量子論理が部分的な無限値ルカシェヴィチ論理として表現できることを数学的に証明しました。これは、従来別個に扱われていた量子論理と多値論理が共通の論理的枠組みで理解できることを示す重要な成果です。量子論理の体系がルカシェヴィチの無限値論理に埋め込めることで、量子命題を多値の真理値で捉える正当性が理論的に裏付けられました。
ファジィ量子論理の提案
ピカチュはさらに、ファジィ量子論理と呼ばれるアプローチを提案しています。このモデルでは、未測定の量子命題を「部分的に真」と扱い、真理値を0から1の連続値で表します。従来の量子論理では複合命題の真理値を直接計算できませんでしたが、ルカシェヴィチ論理モデルでは真理関数的に演算できる利点があります。
量子パラドックスの多値論理的解消
GHZパラドックスへの応用
ピカチュは2015年の研究で、グリーンバーガー=ホーン=ツァイリンガー(GHZ)パラドックスに多値論理を適用しました。このパラドックスは、三つの量子粒子の相関に関する思考実験で、従来の二値論理では矛盾が生じます。
ピカチュの分析によれば、この矛盾は測定前の量子命題に既定の真理値があると仮定したことから生じた擬似的なものです。本来、観測されていない量子対象の性質には二値論理を適用すべきではなく、特殊な否定・論理積・論理和の演算を備えたルカシェヴィチ無限値論理を用いる必要があります。多値論理に基づけば、GHZパラドックスは論理的一貫性を保ったまま解消できることが示されました。
未来の偶発事象としての量子測定
サドベリーの未来時制論理は、ルカシェヴィチが1930年に提起した「未来の偶発事象には0と1の間の真理値を割り当てるべきだ」というアイデアを量子論に応用したものです。量子測定は本質的に未来の事象であり、その結果は測定時まで確定しません。この不確定性を論理的に表現するには、真理値の多値性が不可欠だという洞察は、量子力学における確率の解釈を哲学的に洗練させる試みとして評価されています。
量子計算への応用:三値論理と量子ビット
スタビライザー符号への多値論理の埋め込み
最新の研究として、モリソン・ターナンスキーが2025年に発表したプレプリントでは、量子コンピュータにおける量子ビット(クビット)のエラー耐性を高める文脈で、三値ルカシェヴィチ論理を直接利用する試みが報告されています。
ターナンスキーは、量子誤り訂正用のスタビライザー符号の枠組みに三値ルカシェヴィチ論理(MV3代数)を埋め込むことに成功しました。量子ビットの「0」「1」に加えて、スーパーポジションによる中間状態を論理的第三値として扱えることを示したのです。
重ね合わせ状態の論理的表現
具体的には、クビットの未決定状態(|0⟩と|1⟩の重ね合わせ)をルカシェヴィチ論理の「不定(1/2程度の真理値)」に対応させ、否定や含意などの論理演算を量子ゲート操作として実現する方法が提案されています。このアプローチは、ルカシェヴィチ論理と量子力学との直接の対応関係を確立するものであり、量子アルゴリズムに多値論理的発想を取り入れる新たな道を開いたと評価できます。
ただし、これは非常に新しい試みであり、実際の量子計算機上でその利点や制約を検証するには更なる研究が必要とされています。
多値論理アプローチの意義と課題
量子現象への新たな視座
ルカシェヴィチ多値論理は、量子力学の重ね合わせや観測問題に対して哲学的・理論的に豊かな示唆を与えています。古典的直観にとらわれず真理値の多値性を認めることで、量子現象の論理的記述やパラドックスの解消に寄与できる可能性があります。
特に2010年以降の研究では、無限値論理を用いた量子解釈の提案、量子論理と多値論理の同型対応の発見、さらには量子計算への多値論理応用まで、多方面で進展が見られます。
残された理論的課題
一方で、ボロティンが指摘したように、「どの多値論理体系を選ぶべきか」「論理的多値性から古典的二値性がいかに出現するか」という基本的な問いには、まだ完全な答えが得られていません。量子力学に多値論理を導入すること自体は理にかなっているものの、日常的世界で経験する二値的な事実との接合を整合的に記述するには、さらなる基礎的検討が必要です。
また、パラコンシステント論理(矛盾に寛容な論理)で量子の波動・粒子二重性を扱う試みや、真理値ギャップを認める部分的論理など、他の非古典論理アプローチとの比較検討も重要な研究課題として残されています。
まとめ:多値論理が照らす量子世界の本質
ルカシェヴィチ多値論理を通じて、量子論の不確定性や確率的性質に新たな光を当てる試みは、量子力学の基礎理解と哲学的解釈を深化させるアプローチとして注目されています。真理値の連続的な階調によって量子的曖昧さを直接表現できる点は、量子力学の確率解釈との親和性が高く、重ね合わせ原理を論理的に捉える有力な手段となり得ます。
ピカチュによる量子論理との統合、サドベリーによる未来時制論理の構築、ターナンスキーによる量子計算への応用など、理論的にも実用的にも発展の可能性を秘めた研究が進行中です。量子力学が示す「真でも偽でもない状態」の存在を、論理学の言葉で厳密に表現しようとする営みは、物理学と論理学の境界を越えた知的挑戦として、今後も展開していくでしょう。
コメント