説明可能AI(XAI)が直面する根本的な課題
人工知能システムの意思決定プロセスを人間が理解できる形で説明する「説明可能AI(XAI)」は、AI技術の社会実装において不可欠な要素となっています。しかし、現在のXAI研究には根本的な課題が存在します。
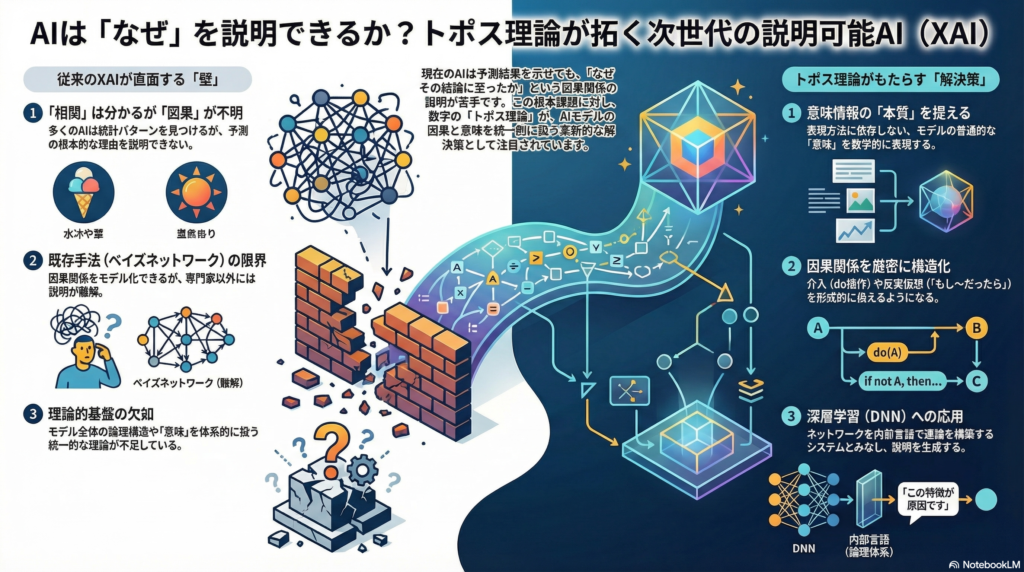
統計的相関を超えた因果的理解の必要性
多くの機械学習モデルは統計的なパターン認識に優れていますが、単なる相関関係の発見にとどまり、「なぜその予測が導かれたのか」という因果的機構を明示することができません。医療診断や自動運転など、高い信頼性が求められる領域では、統計的相関だけでなく因果的な説明が必要不可欠です。XAI研究では、変数間の因果関係を明確にし、モデルの出力に対する意味論的な解釈を提供することが重要視されています。
ベイズネットワークの限界と意味論的解釈の困難さ
ベイズネットワーク(BN)は変数間の因果関係を明示的にモデル化するため、理論上は解釈性の高い枠組みとされています。変数間の依存関係を有向非巡回グラフ(DAG)で表現し、条件付き確率分布を通じて推論を行うこの手法は、因果関係を符号化する自然な枠組みを提供します。
しかし研究者たちは、BNの推論結果を非専門家に分かりやすい形で説明することの困難さを指摘しています。Babakovらの研究によれば、BNは因果関係を伝達する枠組みを提供するものの、一般の人々にとってアクセス可能で意味のある説明を生成することは依然として重大な課題です。従来のXAI手法は局所的な特徴の重要度算出や可視化に偏りがちで、モデル全体の論理構造や意味情報を体系的に扱う理論的基盤が不足しているのです。
トポス理論とは何か:数学的基盤と内部論理
こうした課題を克服する新たなアプローチとして、近年「トポス理論」を用いた理論的枠組みが注目を集めています。
Grothendieckトポスの基本概念
トポス理論は、集合論的な振る舞いを持つ一般的な圏(カテゴリ)を扱う数学の分野です。特にGrothendieckトポスは、すべての有限積・余積、指数対象、部分対象分類子などの構造を備え、その内部に豊かな論理構造を持っています。
トポスの重要な特徴は、内部言語として直観主義的な高階論理を実行できることです。これにより、通常の集合論では表現しにくい複雑な構造や関係性を、形式的かつ体系的に扱うことが可能になります。この性質は、AIモデルの内部構造を論理的に解析し、説明を生成する上で極めて有用です。
意味情報の抽象的表現としてのトポス
数学者オリヴィア・カラメッロは、Grothendieckトポスを「意味情報を表現する抽象的空間」と位置づけています。彼女の理論では、一つの意味(セマンティクス)とそれを表現する様々な公理系(シンタクス)の関係が、トポスとその提示との双対性に対応します。
重要な点は、理論のクラス化トポスがその理論の「意味論的本質」を体現し、異なる公理系表示間でも不変であることです。つまりトポスは、モデルの意味的構造を統一的に表現し、表現方法の違いに依存しない普遍的な「意味」を提供する枠組みとなり得ます。XAIの文脈では、モデル内部の論理や構造をトポスの内部言語として解釈し、それを通じて説明や知識表現を行う可能性が期待されています。
トポス理論による因果モデルの革新的構造化
トポス理論は因果推論の分野でも革新的な応用が進んでいます。
局所因果メカニズムの統合とシーブ構造
Khaderらによる2025年の研究は、トポスが局所的な因果関係を統合し、介入や反実仮想を形式化する上で自然な普遍的性質を備えていることを示しました。
トポスのシーブ構造を用いることで、異なる局所因果関数(独立した因果メカニズム)を整合的にグローバルなモデルに組み合わせることができます。これは従来の因果モデルでは困難だった、複数の独立したメカニズムの統合を数学的に厳密な形で実現します。因果関係が複雑に絡み合う実世界の問題において、この性質は非常に価値があります。
介入操作と反実仮想推論の形式化
因果推論において中心的な概念である「介入」と「反実仮想推論」も、トポス理論の枠組みで形式化できます。
トポスには部分対象分類子という構造が存在し、これを利用して介入操作(do演算)の一般的な定式化が可能です。さらにトポスの内部論理によって、「もし◯◯していたら△△になっていただろう」という反実仮想に関する推論を形式的に扱える基盤が提供されます。
Zhouらのサーベイ論文では、「トポスの内部論理が反実仮想や介入に関する推論の堅牢な基礎を提供する」と指摘されており、これは因果推論の理論的核心を支えるものです。トポス上に因果構造を組み込むことで、従来のベイジアンネットワークや構造因果モデルの枠を超えた、新しい意味論的・代数的な説明生成が見込まれています。
ベイズネットワークとトポス理論の接点
カテゴリ理論による因果構造の再定式化
ベイズネットワークの構造的意味論をカテゴリ理論で捉える試みも進んでいます。Brendan Fongによる2013年の研究は、BNを対称モノイダル圏である「因果理論」として定式化しました。
この枠組みでは、オブジェクトがランダム変数、射が変数間の情報遷移(推論経路)を表します。可測空間と確率測度からなる圏Stochへのモノイダル関手としてモデル化することで、従来のBNを一般化したカテゴリモデルが構築されています。このアプローチにより、BNの因果性や情報フローを代数的・図式的に扱うことが可能となり、より抽象的なレベルでの分析が実現します。
グロタンディーク・トポスを用いた意味的構造表現
さらに2025年のCacioppoの研究では、BNの有限DAG構造に基づくグロタンディーク・トポスが提案されています。この研究は、トポスに内包される構成論理によってネットワークの意味的構造を表現しようとするものです。
BNの有向グラフを射影する圏に対してトポスを構築することで、制約付き論理やセマンティクスを統一的に導入する枠組みが模索されています。これらの研究は、既存のBNに潜む因果・説明構造を高次なカテゴリ的・トポス的文脈で再解釈する道を拓くものであり、因果モデルと意味論的解釈の橋渡しとなる可能性を秘めています。
深層学習への応用:ネットワークの意味機能
DNNのトポス的解釈
トポス理論の知見は、深層ニューラルネットワーク(DNN)の解釈にも新しい視座を与えています。BelfioreとBennequinによる2021年の研究は、任意のDNNをあるグロタンディーク・トポスの対象として扱う理論を構築しました。
彼らの枠組みでは、ネットワークの各層での不変化構造がスタックに対応します。興味深いことに、この研究はネットワークの「意味機能」を、「内部論理に基づく人工言語上で理論を構築し、入力データに関する問いに答える能力」と定義しています。つまりニューラルネットワークは、内部言語で表現される理論を通じて質問への回答(予測結果の説明)を生成するシステムとみなされるのです。
内部言語による説明生成の可能性
この観点に立てば、XAIの説明はモデルの内部で構築される論理的理論とみなすことができ、トポスの内部言語がその理論表現手段となります。カラメッロらの「意味情報としてのトポス理論」の視点を踏まえれば、モデルに内在する知識や意味内容を高階論理で表現し、その結果を説明として出力する枠組みが理論的に期待できます。
具体的には、入力と出力を結ぶ因果関係を内部論理で表現し、そこから人間が理解可能な形式で理論を抽出するという、より体系的な説明生成の道が拓ける可能性があります。これは従来の特徴量の重要度に基づく説明とは質的に異なる、より本質的な説明手法となり得ます。
今後の研究方向性と実装への課題
トポス理論をXAIに応用する枠組みはまだ発展途上ですが、有望な方向性がいくつか示されています。
第一に、トポスを用いた形式論理によってモデルの予測を「なぜそうなるか」論理的に説明する手法の構築です。反実仮想的な問いや推論規則を自然に記述できるトポスの内部論理は、説明生成の強力なツールとなる可能性があります。
第二に、内部言語と自然言語説明との対応づけです。抽象的な論理構造を一般の人々が理解できる自然言語に変換する橋渡しの仕組みが必要となります。
第三に、マルコフ圏や他の確率的圏との統合です。確率的推論と論理的推論を統一的に扱える枠組みの構築は、実用的なXAIシステムの実現に不可欠でしょう。
一方で、未踏の課題も多く存在します。これら抽象的な枠組みを実際のデータ駆動学習モデルにどのように適用・実装するかは大きな技術的チャレンジです。また既存の説明生成手法(局所的特徴寄与など)との差分をどのように定量的に評価するかも重要な研究課題となります。
ネットワークの不変構造やスキーマに対するトポス的理解と、人間の持つ意味付けとの橋渡し、すなわち意味論的整合性の問題も大きな挑戦です。現在提案されているトポス理論的枠組みは主に理論的であり、実証実験や大規模データへの適用はまだ限られています。
今後は理論と実践の両面から検証と拡張が必要であり、トポスの内部論理を活用した形式的説明がどの程度実用的かを明らかにする研究が期待されます。さらに、トポスとホモトピー理論などの高次構造を組み合わせた知識表現や、動的・時系列データに対するコシーブ的モデリングなど、さらなる未踏領域も広がっています。
まとめ:理論的深みがもたらす新たな地平
トポス理論は、説明可能AI(XAI)における因果性と意味論の統一的な枠組みを提供し得る可能性を秘めています。従来のXAI研究が局所的な特徴の可視化や重要度算出に焦点を当ててきたのに対し、トポス理論的アプローチはモデルの論理構造全体を体系的に扱う理論的基盤を提供します。
ベイズネットワークをカテゴリ理論やトポスの枠組みで再定式化する研究、深層学習モデルの意味機能をトポスの対象として捉える試み、因果推論における介入や反実仮想をトポスの内部論理で形式化する研究など、多様なアプローチが進展しています。
実験的検証はまだ限定的ですが、理論的な深みという点で既存研究との大きなギャップを埋める道筋を示しています。今後、理論の精緻化と実装技術の進展により、トポス理論に基づく次世代のXAIシステムが実現される可能性があるでしょう。数学的厳密さと実用性を両立させた説明可能AIの実現に向けて、この分野の更なる発展が期待されます。
コメント