量子確率モデルとは何か——認知科学における「重ね合わせ」の意味
私たちが何かを迷い、複数の選択肢を同時に考慮しているとき、脳の中では何が起きているのか。この問いに対して、近年「量子確率モデル(quantum-like models)」というアプローチが新たな視座を提供している。
ただし、重要な前置きがある。量子確率モデルとは、脳が物理的な量子コンピュータとして動いているという主張ではない。それはあくまで「確率の幾何学」として、認知現象を記述するための数学的枠組みである。文脈依存性、順序効果(質問の順番で答えが変わる現象)、全確率の法則の破れといった行動データの特徴を、ヒルベルト空間上の状態ベクトルや干渉項で説明しようとするものだ。
本記事では、この量子確率モデルの数学的定義を整理し、神経科学側で観察されている「重ね合わせに似た現象」との対応関係を検討する。さらに、MEGや光遺伝学を用いて両者の橋渡しを検証する実験プロトコルまで踏み込んで解説する。
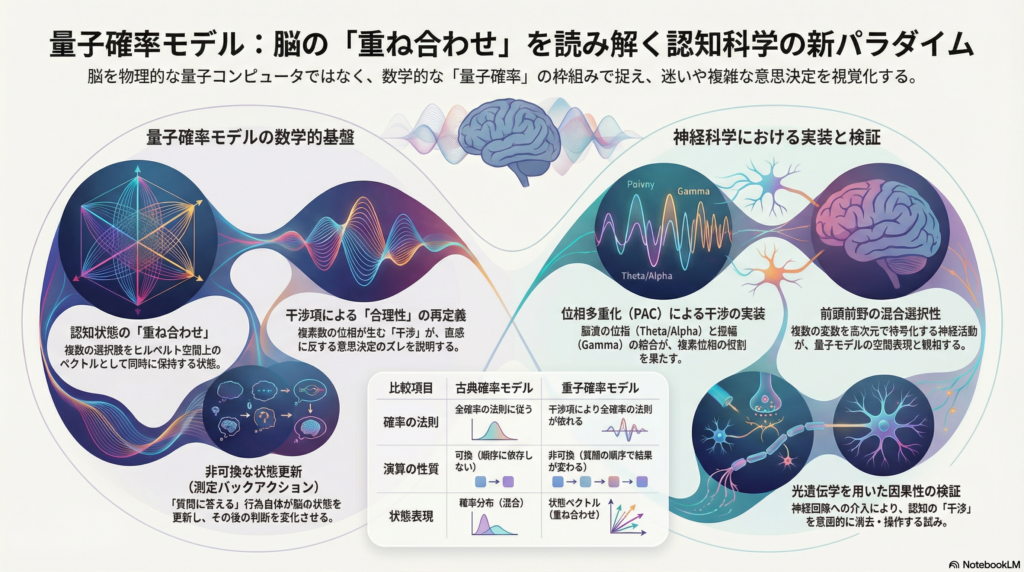
ヒルベルト空間における重ね合わせ状態の数学的定義
純粋状態と線形結合——認知を「ベクトル」で表す
量子確率モデルの出発点は、認知状態をヒルベルト空間 H 上の単位ベクトル ∣ψ⟩(純粋状態)として表現することにある。
ある基底(たとえば回答カテゴリや仮説の集合){∣i⟩} に対して、状態は次のように書ける。 ∣ψ⟩=i∑ci∣i⟩,i∑∣ci∣2=1
この「複数基底状態の線形結合」が重ね合わせ(superposition)である。古典確率の「混合(mixture)」と根本的に異なるのは、各係数 ci が複素数であるという点だ。複素数は実部と虚部を持ち、その「位相」が干渉項を生む源泉となる。
密度行列——混合とコヒーレンスを統一的に扱う
現実の認知状態は、純粋な重ね合わせよりも不純な「混合状態」で表されることが多い。その場合は密度行列 ρ が用いられる。
密度行列の対角成分は古典的な確率分布に対応し、非対角成分(オフダイアゴナル要素)は量子的なコヒーレンス——すなわち基底間の位相相関——を表す。古典混合は対角成分のみで説明できるが、真の重ね合わせには非対角成分が存在し、これが干渉効果の数学的根拠となる。
ボルン則と測定バックアクション
観測(質問や課題)を射影演算子 ΠA で表すと、回答確率は次のように与えられる。 P(A)=⟨ψ∣ΠA∣ψ⟩またはP(A)=Tr(ρΠA)
重要なのは、認知モデルにおいて「質問に答える」という行為が状態を更新する(測定バックアクション)という点だ。この更新の仕方が非可換——つまり AからB の順に質問するか、B から A の順に質問するかで異なる結果を生む——ことが、心理実験で観察される順序効果と対応している。
干渉項——全確率の法則が破れる理由
古典確率では、中間状態 A/¬A を経由して B を予測するとき、以下の「全確率の法則」が必ず成立する。 P(B)=P(B∣A)P(A)+P(B∣¬A)P(¬A)
しかし量子確率では、複素振幅の線形結合を展開すると、古典項に加えて次の干渉項が現れる。2Re(α∗β⟨A∣ΠB∣¬A⟩)
この余分な項——正にも負にもなりうる——が、実験で観察される「全確率の法則からのズレ」を説明する核心である。
神経科学における「重ね合わせ類似現象」の実証的証拠
混合選択性と高次元表現——前頭前野の柔軟な符号化
前頭前野(PFC)の研究では、単一ニューロンが「刺激×文脈×ルール×目標」といった複数の変数の組み合わせに応答するという「混合選択性(mixed selectivity)」が繰り返し報告されている。
この高次元な表現空間は、量子確率モデルが想定するヒルベルト空間の「基底(観測)選択に応じて射影が変わる」という操作的直観と親和的だ。課題が進むにつれ表象が「形を変えつつ保持される(code-morphing)」という報告も存在し、同一の情報内容が複数のサブスペースにまたがって保持される様相は、重ね合わせの見かけを作る有力な神経基盤と考えられる。ただし、これが物理的量子性を必要とするわけではない点は強調しておく必要がある。
確率分布としての神経表象——不確実性の符号化
感覚皮質や視覚系では、刺激値だけでなくその不確実性を含む確率分布が神経活動に埋め込まれているという枠組みが発展してきた。ヒト視覚皮質の fMRI パターンから刺激に関する確率分布(不確実性)を復元し、行動がその分布を利用していることを示す研究がある。
この「確率分布を表象する」能力は、量子確率モデルが前提とする「状態が確率を生成する」という枠組みの神経的実装候補として注目される。動物電気生理での「確率的集団符号化(probabilistic population codes)」研究も、密度行列の対角成分に相当する古典混合状態の神経基盤を示すものとして位置づけられる。
位相多重化——干渉の神経実装として最も具体的な候補
量子確率における干渉に不可欠なのは「複素振幅の位相」である。神経系でこれに最も対応しうるのが、シータ(theta)波やアルファ(alpha)波などの振動位相と、ガンマ(gamma)帯域の高周波活動との「位相‐振幅結合(PAC: Phase-Amplitude Coupling)」だ。
短期記憶課題において、複数の対象情報が特定の振動位相に依存して強く表現される「位相依存符号化(phase-dependent coding)」が報告されており、「theta–gamma コード」と呼ばれる複数項目の時間分割保持仮説を支持する結果が積み重なっている。この位相結合が複素振幅の「位相」に対応しうるため、干渉項を生成する神経機構の最有力候補として理論化しやすい状況にある。
サンプリング仮説——重ね合わせの代替説明
皮質活動の試行間変動や自発活動を、確率推論のサンプリング(MCMC等)として解釈する理論も有力だ。膜電位を対数オッズに対応づけ、ネットワークダイナミクスが所望の確率分布からのサンプル列を生成するという構成は、スパイキング回路で実装可能であることが示されている。
この観点では「複数仮説が同時に重ね合わさる」ではなく「時系列でサンプルが出入りする」として現象を説明することになり、密度行列でいう混合(デコヒーレンスした状態)と整合的な対応づけが可能だ。
光遺伝学と状態遷移——測定バックアクションの因果証拠
量子確率モデルでは、測定が状態を更新し、その更新が後続の確率を変える。神経科学では、集団状態がアトラクタへ収束し、光遺伝学的摂動に対してロバストでありながら、一定条件では別の安定状態へスイッチしうることが示されている。この「摂動が状態を別アトラクタへ切り替える」という因果像は、量子モデルの「測定が状態を変える(測定バックアクション)」と操作的に強く類似している。
数学構造と神経要素の対応可能性——支持と反証
量子確率モデルの各要素と、神経学的対応候補を整理すると以下のようになる。
状態ベクトル ∣ψ⟩|\psi\rangle ∣ψ⟩ に対応する神経要素 として最有力なのは、前頭前野や連合皮質で観測される高次元集団活動ベクトル(発火率ベクトル)や低次元潜在状態だ。支持根拠は十分にあるが、「基底の選択が何に対応するか」を操作的に定義することが難しいという難点がある。
密度行列 ρ\rho ρ に対応する神経要素 の候補としては、不確実性を表す確率分布(PPC)、2次統計(共分散・相関)、試行間変動を通じた分布表象などが挙げられる。しかし、非対角成分(位相コヒーレンス)に対応する観測量を自明に特定することが難しく、密度行列推定の識別性が根本的な問題として残る。
干渉項に対応する神経要素としては、位相差を持つ振動要素の合成、興奮性・抑制性(E/I)相互作用による競合と抑制、非線形な混合(ゲイン制御)が候補となる。ただし、行動レベルの「全確率の法則の破れ」は、注意・記憶・戦略の混合といった古典的要因でも生じうるため、干渉を量子的なものと直接同一視することはできない。
非可換な状態更新に対応する神経要素としては、再帰回路ダイナミクス、状態依存ゲーティング、短期可塑性、読出しによる状態の再符号化が候補となる。前頭前野での文脈依存計算がRNNダイナミクスとして説明されることは、非可換風の現象が古典ダイナミクスで生じることの好例でもあり、量子モデルの優位性を主張するには識別的な介入実験が必要になる。
検証実験プロトコル——MEG・多点記録・光遺伝学の活用
プロトコル①:位相干渉仮説のヒトMEG/EEG検証
健常被験者で順序効果が強い質問系列課題(または全確率の法則の破れが出る二段階意思決定課題)を実施し、同時に MEG・高密度 EEG(可能なら頭蓋内 ECoG)を計測する。
各試行で前頭‐頭頂間の位相同期および theta/alpha 位相と gamma パワーのクロス周波数結合を推定し、行動から推定した干渉パラメータの試行間変動と結びつける。モデル比較として、量子確率モデル、古典ベイズ+注意変動モデル、Markov/RNN 由来の履歴依存モデルを同一行動データに当てはめ、神経指標を共変量に加えたときに量子モデルの説明力が特異的に改善するかを検証する。
期待される結果は、「試行開始前〜問い合わせ直前の位相状態が干渉項の符号・大きさを予測する」というものだ。これが確認されれば、「複素位相が干渉に必要」という実装論と整合する。
プロトコル②:非可換な状態更新写像の同定(動物・多点記録)
マカクまたはマウスで、文脈(ルール)によって同一刺激が別の判断に写像される課題を設計する。前頭前野・頭頂・感覚皮質から同時多点記録し、「問い合わせA後の状態遷移写像 UA」と「問い合わせB後の写像 UB」を介入なし条件で同定する。
UA∘UB と UB∘UA が統計的に異なるか(非可換性)を、状態軌道距離・予測誤差・ヤコビアン差などで評価する。行動上の順序効果の大きさと更新非可換性指標の相関が示されれば、量子測定理論的整理を支持する証拠となる。
プロトコル③:干渉の因果消去(光遺伝学・E/I操作)
行動上の順序効果・全確率破れが安定して出る条件を確立したうえで、前頭‐感覚間の位相結合を崩す介入(特定帯域のリズム生成回路への抑制、または位相振幅結合に寄与しうる回路要素の操作)を行う。
もし位相結合が干渉の必要条件であれば、この介入により行動の干渉項だけが減衰し、全確率の法則に近づくはずだ。遅延期の集団状態が離散端点へ向かい、摂動で別端点へ切り替わるという先行知見を活用し、問い合わせ直前の短い摂動が順序効果の符号や大きさをどう変えるかをテストすることも有力なアプローチだ。
代替説明との比較——古典的説明の射程
量子確率モデルが説明しようとする現象は、少なくとも三種類の古典的説明でも産出されうることに注意が必要だ。
第一に、再帰ネットワークや確率過程(Markov 過程を含む)は、履歴依存と文脈依存を自然に生む。前頭前野の文脈依存計算が RNN ダイナミクスで説明されること自体が、非可換「風」の現象が古典動力学で生じうることの証拠でもある。
第二に、「混合選択性+高次元表現+読出しの選択」の組み合わせにより、同一集団から状況依存で異なる情報が読み出され、結果として順序・文脈依存の確率変化が生じる。この説明は神経実装として強力だが、量子的な干渉項(位相に依存する符号反転等)を必須としない。
第三に、ノイズ・戦略混合・注意変動などにより、集計された行動確率が全確率の法則から見かけ上ずれる可能性がある。「量子モデルの適合がパラメータの柔軟性に過ぎないのではないか」という批判は根強く存在する。
こうした理由から、神経機構の解明には、モデル当てはまりだけでなく、介入によって「干渉だけを選択的に変化させる」識別実験が不可欠である。
まとめ——重ね合わせの神経実装研究の現在地と課題
量子確率モデルにおける重ね合わせ状態は、ヒルベルト空間上の線形結合(純粋状態)あるいは密度行列(混合を含む一般状態)として厳密に定義でき、干渉項と非可換な状態更新写像が、認知・行動データの文脈依存性を説明する核となる。
神経科学側では、混合選択性・確率分布符号化・サンプリング・位相多重化・アトラクタ遷移といった現象が多階層で観測され、特に「位相+E/I相互作用+履歴依存更新」が干渉と非可換更新の実装候補として具体性を帯びてきた。しかし、多くは古典確率・動力学でも説明可能であり、決定的な前進のためには次の優先事項が残されている。
まず、行動干渉(全確率の法則の破れ)と神経位相指標の結合を、事前登録・複数ラボ再現で確立することが急務だ。次に、動物実験で更新写像の非可換性を状態空間モデルとして同定し、介入で選択的に操作できる実験系を構築する必要がある。さらに、密度行列に相当する統計量(共分散・クロススペクトルなど)を「測定に依存する状態」として推定する手続きの標準化が求められる。最終的には、ヒルベルト空間に拘らない一般化確率理論(GPT)的枠組みで神経ネットワークを記述し、どの条件でヒルベルト型が必要になるかを反証可能な形で定式化することが目標となる。
量子確率モデルと神経科学の対話は、「脳が量子コンピュータである」という問いではなく、「認知の確率的幾何学を、古典的な神経回路がいかにエミュレートするか」という問いとして進展しつつある。この研究フロンティアは、認知科学・神経科学・量子情報理論の交差点に位置し、今後の実験的・理論的進展が強く期待される領域だ。
コメント