はじめに
現代の人工知能研究は、深層学習の実用性と記号AIの論理性という二つの方向性の間で揺れ動いている。一方で、量子計算の分野では、トポロジカル量子計算という新しいパラダイムが、エラー耐性を持つ量子コンピュータの実現可能性を示している。これら一見無関係に見える研究領域を結びつける鍵が、**圏論(Category Theory)**という数学的枠組みである。
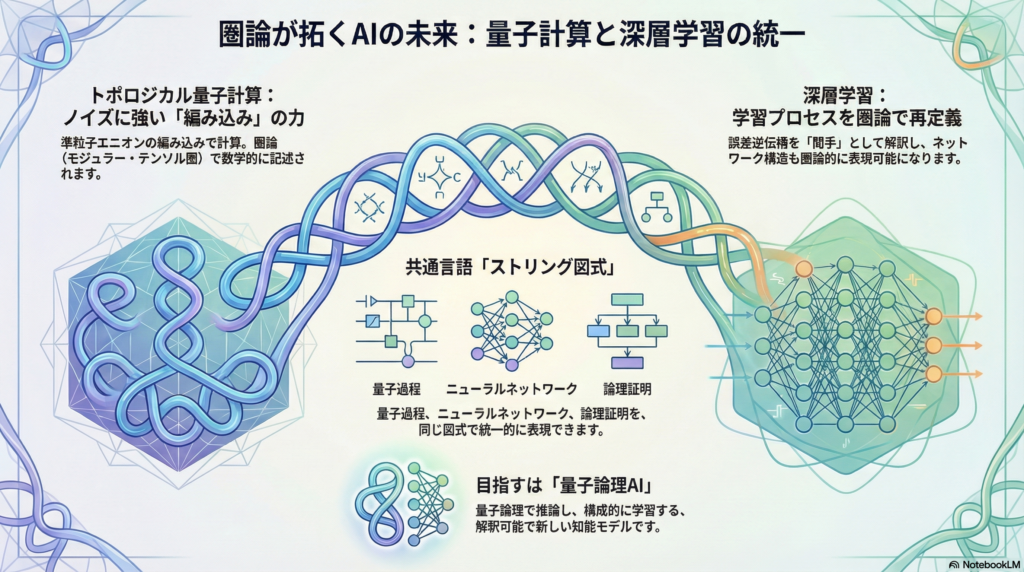
本記事では、トポロジカル量子計算における圏論的基礎、深層学習の圏論的記述、そして量子論理とAIを橋渡しする統一的推論フレームワークの可能性について解説する。
トポロジカル量子計算における圏論的基盤
エニオンとブレイド群による量子情報処理
トポロジカル量子計算(TQC)は、エニオン(anyons)と呼ばれる特殊な準粒子に量子情報を符号化し、それらの編み込み(braiding)操作によって量子ゲートを実装する計算モデルである。エニオンの最も重要な特徴は、通常のボース粒子やフェルミ粒子とは異なり、その統計性がブレイド群によって支配される点にある。
この性質により、エニオンの交換操作はトポロジカルに保護され、局所的な環境ノイズに対して本質的な耐故障性を持つ。つまり、量子ゲートの実装がトポロジー不変量として実現されるため、小さな摂動では計算結果が変化しない。これは、従来の量子計算における最大の課題であるデコヒーレンス問題への根本的な解決策となる可能性がある。
モジュラー・テンソル圏による数学的定式化
エニオン系の厳密な数学的記述は、**モジュラー・テンソル圏(Modular Tensor Category)**という圏論的構造によって与えられる。この圏論的枠組みでは:
- **対象(objects)**が異なる種類のエニオン粒子型を表現する
- **射(morphisms)**が物理過程やエニオンの合成状態を記述する
- モノイド積がエニオンの融合規則を捉える
- 編み込み構造がエニオンの交換操作に対応する
この定式化により、エニオンの超選択規則や統計性が自然に表現される。特筆すべきは、単一のエニオンは独立したヒルベルト空間を持たないが、複数のエニオンの組み合わせは明確なヒルベルト空間を形成するという、量子力学における非局所性の表現が可能になる点である。
高次圏構造による計算モデルの分離
近年の研究では、TQCを記述するために2つの異なる圏を明確に区別する必要性が指摘されている:
- 物理的エニオン圏:エニオンの種類、融合規則、編み込み規則を記述する編み込み融合圏
- 計算圏:有限次元ヒルベルト空間と線形写像からなる部分圏で、実際の計算状態と操作を表現する
Ahmadi(2025)による編み込み融合2圏の導入は、これらを統合する高次圏構造を提供した。この2圏構造では:
- 0射がエニオン型を表す
- 1射が相互作用のヒルベルト空間モデルを表す
- 2射が融合行列や編み込み行列を表す
この分離により、従来のアプローチで混同されていたエニオンの融合(0射レベル)とベクトル空間のテンソル積(1射レベル)が明確に区別され、理論的整合性が向上している。
トポロジカル量子場理論との接続
TQCの圏論的視点は、トポロジカル量子場理論(TQFT)に深く根ざしている。Atiyahの関手的アプローチに従えば、TQCプロトコルはトポロジカルな軌道(ブレイドやコボルディズム)の圏からヒルベルト空間の圏への関手として理解できる。この関手は、トポロジカル過程にベクトル空間と線形写像を割り当て、物理的実装と数学的構造を結びつける。
深層学習の圏論的記述と関手的学習
誤差逆伝播の関手的解釈
深層学習は工学的発展を遂げてきたが、その数学的基盤は必ずしも明確ではなかった。Fong、Spivak、Tuyéras(2019)による「Backpropagation as Functor」は、学習過程を圏論的に再解釈する画期的な研究である。
この枠組みでは、ニューラルネットワークがパラメータの圏からデータの圏への関手として捉えられ、誤差逆伝播が関手的構成として自然に導出される。具体的には、前向き計算と後向き計算の両方を扱うレンズ(lenses)やオプティクス圏と呼ばれる二重圏的構造で定式化される。
この視点により、勾配更新は単なる計算手順ではなく、圏論的双対性を持つ構造的操作として理解できる。
ニューラルアーキテクチャのモノイド構造
ニューラルネットワークの構造は、データ変換を表すモノイド圏における射として自然に表現される。順伝播ネットワークは射の合成:f=fn∘⋯∘f1
として記述され、並列なサブネットワークはテンソル積で表現できる。この視点により、複雑なニューラルアーキテクチャの構成原理が代数的に明確化される。
関手的学習パラダイムの展開
近年提案されている**関手的学習(Functorial Learning)**は、単純な関数 X→Y の学習を超えて、 圏 C\mathcal{C} C からベクトル空間の圏への関手そのものを学習対象とする という新しいパラダイムである。
量子自然言語処理(QNLP)における応用では、文法構造を表す圏から量子回路や実ベクトル空間へのモノイド関手を学習することで、文の意味を計算的に表現する。これにより、文法的構造(論理構造)を保持したまま、量子回路のパラメータをデータから最適化することが可能になった。
この「文法=エンタングルメント」という考え方は、論理的結合が量子的エンタングルメントに対応するという深い洞察を提供する。
層理論と深層学習の拡張
圏論は層理論(Sheaf Theory)を通じても深層学習に応用されている。層は局所情報から大域情報を構成するための数学的道具であり、これを用いた層ニューラルネットワークがグラフニューラルネットワークの一般化として提案されている。
この手法により、有向グラフや符号付きグラフなど、異種関係や制約を持つデータにおいて、従来のGNNを超える性能が実証されている。層の前層条件と貼り合わせ条件が、グラフ構造における情報伝播の自然な制約として機能する。
量子論理と圏論的AIを結ぶモノイド圏
量子論理の認知モデルとしての有効性
量子論理は、ヒルベルト空間の部分空間格子に基づく非分配的論理であり、文脈依存的な真理値を表現できる。この特性は、人間の認知や推論のモデルとしても有効であることが示唆されている。
人間の推論は古典論理の分配律や排中律をしばしば違反する。たとえば、文脈に応じて概念の意味が変化する現象や、順序効果を示す判断過程は、量子論理の枠組みで自然に記述できる可能性がある。
ストリング図式による統一的表現
量子論理と圏論的AIを結ぶ鍵は、モノイド圏とストリング図式である。同一の図式的表現が、論理証明、古典計算、量子過程を、関手による写像先の違いとして統一的に表現できる。
DisCoCatモデルでは、文法(論理構造)を剛モノイド圏の射とみなし、それを有限次元ヒルベルト空間の圏への関手で写すことで、量子回路や線形写像として実装する。この枠組みにより、自然言語の構成的意味論が量子計算として実現される。
ZX計算と量子図式論理
ZX計算などの量子図式計算は、量子論理における証明体系とも解釈できる。こうした図式論理は**圏論的量子力学(CQM)**と深く関係し、AI推論への応用が探索されている。
重要な観察は、量子回路とニューラルネットワークの双方がモノイド圏の射であるという点である。最近の研究では、ストリング図式上で微分を定義する「図式的微分」により、量子変分回路とニューラルネットワークの学習が同一の枠組みで扱えることが示されている。
統一的推論・学習フレームワークの可能性
量子論理的AIの構想
これらの要素を統合すると、量子論理と圏論的学習意味論を融合した統一的推論体系の可能性が見えてくる。この枠組みは、記号AIの脆弱性とブラックボックス的深層学習の解釈不可能性という両極端を超え、構成的で解釈可能な量子風推論AIを目指すものである。
具体的には:
- 知識ベースを量子論理的トポスとして表現する
- 学習を文脈から結果への関手更新として捉える
- 推論を射の合成として実行する
といった統一的アーキテクチャが考えられる。
圏論的論理の道具立て
層理論、モナド、随伴関手など、圏論的論理が提供する豊富な道具は、論理制約と学習を統合するための強力な構文・意味論を提供する。Gavranovićら(2024)の研究は、2圏とモナドを用いてニューラルアーキテクチャを統一的に記述しており、論理制約への拡張可能性を示唆している。
このアプローチでは、異なる抽象レベル(データ、モデル、メタ学習)が高次圏の異なる次元として表現され、それらの間の一貫性が随伴関手や自然変換によって保証される。
非古典論理で推論する知能
量子論理に基づくAIは、古典的な真偽値論理を超えた推論能力を持つ可能性がある。文脈依存性、非可換性、エンタングルメントといった量子的特性が、人間の創造的思考や直観的判断をより適切にモデル化できるかもしれない。
ただし、これは投機的な可能性であり、実証的検証が必要である。現段階では、圏論的枠組みが異なる計算パラダイムを統一的に記述する言語を提供している、という点が確実に言える成果である。
まとめ:新しい知能モデルへの道
本記事で概観した研究動向は、以下の重要な示唆を含んでいる:
- 量子計算の理論基盤:モジュラー・テンソル圏や編み込み2圏による成熟した数学的定式化が、トポロジカル量子計算の実現可能性を支えている
- AIの圏論的再構築:深層学習が関手的学習として再定式化されることで、構成的・解釈可能な機械学習の基盤が整いつつある
- 論理と計算の統一言語:モノイド圏とストリング図式が、論理証明、古典計算、量子過程を横断する共通言語を提供する
- 統一的知能理論の萌芽:量子論理で推論し、構成的に学習するAIという新しい知能モデルへの理論的道筋が見えてきた
これらの発展は、非古典論理で推論し、構成的に学習する知能という新しいパラダイムへの道を開く可能性を秘めている。ただし、理論的可能性と実用的実装の間には依然として大きなギャップがあり、今後の学際的研究によって橋渡しされる必要がある。
圏論という抽象的な数学言語が、量子物理学、計算科学、人工知能という異なる領域を結びつける統一的視点を提供していることは確かである。この統一的視点が、次世代の計算パラダイムと知能モデルの基盤となる可能性に、今後も注目していきたい。
コメント