量子モデルとは何か——「脳が量子コンピュータ」ではない
量子認知(quantum cognition)という言葉を聞いて、「脳内で量子現象が起きている」という主張を想像する人は少なくない。しかし研究の実態は大きく異なる。量子モデルが目指すのは、量子力学の数理的枠組み——とりわけ量子確率・量子測定理論・ヒルベルト空間——を、「人間の認知がもつ文脈依存性や順序依存性」を記述する形式主義として活用することだ。
古典的な確率論(コルモゴロフ確率)では、事象を集合として扱い、確率を集合の測度として定義する。一方、量子的な枠組みでは、事象を部分空間(射影)として表し、確率を「状態と事象の幾何学的重なり」として定義する。この違いが生む最大の特徴は、測定(=質問)の順序が結果の確率構造を変えうるという非可換性にある。
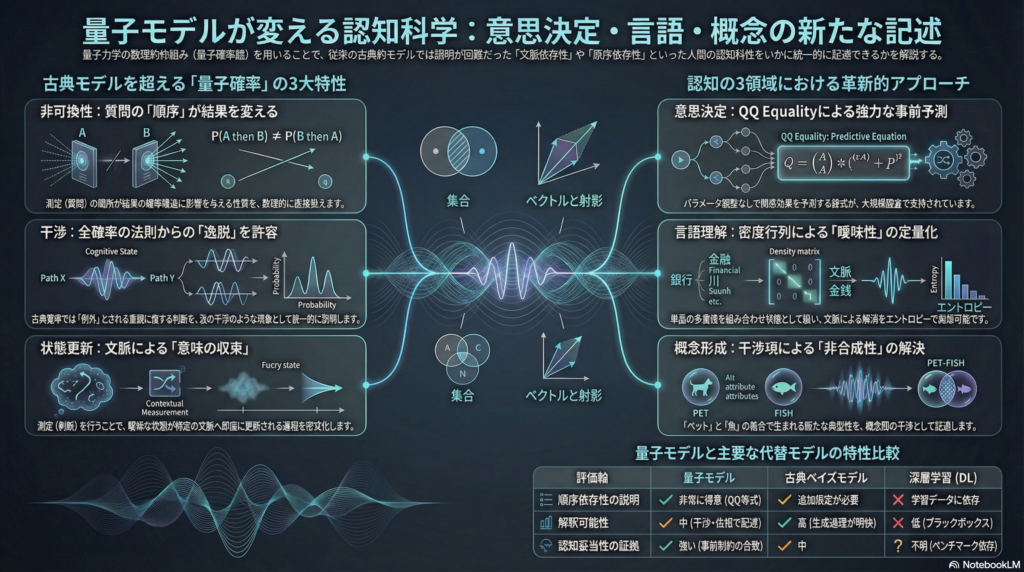
具体的には、①非可換性(順序依存)、②干渉(全確率の法則からの逸脱)、③状態更新(測定による文脈生成)という三つの性質を、単一の形式主義のなかで自然に扱えることが、古典確率やベイズモデルに対する量子モデルの主な優位点とされる。
本記事では、こうした量子(ライク)モデルが①意思決定、②言語理解、③概念形成という三つの認知領域にどのように適用されるのかを、2006年以降の研究を参照しながら批判的に整理する。
意思決定への量子確率モデル——QQ equalityという強い制約
なぜ古典確率では不十分なのか
意思決定研究において、古典確率(コルモゴロフ)や標準的な合理性原理(期待効用理論・Sure-Thing Principle・全確率の法則)から系統的に逸脱する現象は長年報告されてきた。連言錯誤(conjunction fallacy)、選言効果(disjunction effect)、質問順序効果などがその代表例だ。
古典的なアプローチでは、これらの逸脱をそれぞれ個別の「例外則」として処理することが多かった。量子確率モデルが提案するのは、それとはまったく異なる方向性——これらの逸脱を「非可換な射影に起因する干渉」として、同一の確率公理系のなかで統一的に説明することだ。
QQ equalityという事前・パラメータフリーの予測
量子モデルが意思決定研究にもたらした最も重要な貢献のひとつが、QQ equalityと呼ばれる制約である。
QQモデルでは、二つの質問AとBを「A→B」の順で聞いた場合と「B→A」の順で聞いた場合の回答確率の間に、事前に(パラメータ調整なしに)成り立つべき等式制約を導出できる。これは、「当てはまりが良い」という事後的な説明とは性格が根本的に異なる。等式が事前に予測され、データによって検証される——この点が証拠基盤として相対的に堅牢とされる理由だ。
実際、複数の全国代表調査を含む大規模検証において、この等式制約の成立が支持されたと報告されている。古典確率やベイズ的枠組みでは、順序効果を説明するために追加の仮定が必要になることが多く、QQ equalityのような制約を自然に導出するのは困難とされる。
意思決定モデルの比較と限界
量子モデルが「どの程度優れているか」を問うためには、当然ながら古典的代替モデルとの公平な比較が必要になる。動的不整合の説明においては、量子モデルとベイズ的モデルをモデル選択基準で比較し、精度・簡潔性・頑健性の観点から量子モデルに有利な結果を示した研究も存在する。これは「自由度が高いから当たる」という批判に対して、モデル比較を明示的に導入する点で意義が大きい。
一方で限界も明確に存在する。まず、どのヒルベルト空間を採用するか(次元・基底・射影の意味付け)が設計問題として残り、モデルを比較可能な形で標準化しにくい。また、量子モデルの特定クラス(非縮退モデル)が満たすべき別の制約(GR方程式)が多くのデータセットで破れるという批判的検討もある。QQ equalityが成り立つだけでは「どの量子モデルでもよい」とはならないことも、重要な注意点だ。
さらに、順序効果と「同じ質問を繰り返すと同じ答えを言いがち(回答再現効果)」の両立は、基本的な射影測定では困難であり、量子インストルメントと呼ばれる一般測定への拡張が必要になるという「測定理論側の未整理」も残っている。
選言効果については、近年の大規模再現研究で「パラダイムによって再現度が異なる」ことが示唆されており、量子モデルが「干渉が出る条件」を理論的に特定できるかどうかが今後の鍵となる。
言語理解への量子形式主義——曖昧性を密度行列で表す
語義曖昧性と量子的重ね合わせ
言語理解において量子形式主義が注目されるのは、語義曖昧性(polysemy)の扱いにおいてだ。「銀行(bank)」という単語は「金融機関」と「川岸」という複数の意味を持つが、文脈によって解釈が一意に定まる。この「複数の意味が重なり合った状態から、文脈によって収束する」という過程は、量子力学の重ね合わせと測定のアナロジーとして自然に捉えられる。
量子形式主義の言語応用では、単語を単一のベクトルではなく密度行列(混合状態)として表すモデルが提案されている。密度行列は複数の意味状態の「混合」を表現できるため、曖昧性を一括して扱うことが可能になる。そして合成(文脈中での使用)により曖昧性が解消されるという過程を、状態の更新として形式化できる点が利点とされる。さらに、曖昧性の量をフォン・ノイマンエントロピーで定量的に測れるという副産物もある。
圏論的合成モデルとNLP評価
文法構造と分布意味論を結合するDisCoCat(分布意味×圏論)系譜では、文の意味を語の意味の圏論的合成として計算する枠組みが提案されてきた。実装研究では、圏論的合成モデルが人手による類似度判断との相関においてベースラインを上回ることが示されている。
具体的には、他動詞文の類似度課題においてSpearman相関係数で乗算ベースのモデルを上回る結果が報告されており、評価指標(相関指標 vs 平均差)の選択が結論に影響しうることも、論文自体が明示している。曖昧性解消タスクでも、密度行列を用いた複数の構成が比較検討されており、特定の組み合わせ(multi-sense Word2DM+Phaser)が強い性能を示すと報告されている。
量子回路を活用するQNLP(量子自然言語処理)では、文法構造を量子回路に写像することで計算優位が生まれる可能性も議論されているが、現状はNISQ(ノイズあり中規模量子)制約下での実験規模が限定されており、古典テンソルネットワークとの総合コスト比較が不可欠な段階にある。
認知妥当性という根本的課題
言語の量子モデルが抱える最大の課題は、NLPベンチマーク上の改善が「人間のオンライン言語処理」を説明したことにはならないという点だ。読文時間・視線追跡・事象関連電位(ERP)といった心理言語学的測定との接続は、依然として発展途上にある。NLPで成功したモデルが認知的に妥当であるとは限らず、この二つを区別することが研究の前進に不可欠だ。
また、密度行列を導入すると名詞が行列に、動詞が高階テンソルになるため、表現次元が急増する。実用的な応用には低ランク化・近似・回路化といった手法が必要になる。
概念形成への量子モデル——過拡張と干渉
概念結合の非合成性という古典的問題
「ペット(pet)」と「魚(fish)」はそれぞれ典型例を持つが、「ペットの魚(pet fish)」は両方の典型例とは異なる独自の典型像を持つ。これがpet-fish問題と呼ばれる現象で、概念結合の意味が単純な論理演算(集合の積・和)では説明しきれないことを示す。
量子モデルは、こうした概念結合の非合成性を「干渉」として表現しようとする。二つの概念を重ね合わせ状態として表し、結合概念での典型性・選好評価の逸脱を干渉項で記述するアプローチだ。
Hamptonデータによる定量的検証
古典的な実験として、Hamptonによる結合概念での過拡張(conjunctive overextension)研究がある。結合概念の成員性判断がブール的合成に従わないことが実証されており、量子モデルはこのデータを干渉の枠組みで説明しようとする。
具体的には、「Furniture(家具)」と「Household Appliances(家電)」およびその結合概念を扱ったモデルでは、16の例を17次元ヒルベルト空間で表現し、結合確率が古典的基準からずれる様子を干渉角で記述している。注目すべき定量的観察として、結合概念の確率は「ファジィ集合のmin」よりも「二概念確率の平均」に近いことが示されており、結合概念との相関も平均(0.899)がmin(0.795)を上回る。この観察は、「and」による概念結合が直観的な論理演算そのものとして機能していない可能性を示唆する。
量子類似性モデル(QSM)では、概念を部分空間として、心的状態をベクトルとして表し、類似性を逐次射影として計算する。この枠組みでは、射影の順序によって類似性の非対称性が自然に生まれる点も特徴的だ。
自由度と検証可能性のトレードオフ
概念形成の量子モデルが直面する最大の批判は、モデルの自由度が高すぎるという点だ。高次元化や複数セクターを許容すれば、多くのデータに当てはめることが可能になるが、それは「何でも説明できる」というモデルの弱さを意味する。
このため、外部データへの一般化・パラメータ固定での予測、あるいは事前制約(等式・不等式)に基づく検証が必須になる。新規予測の事前登録と、古典的なプロトタイプ理論・エグザンプル理論との公平な比較が、今後の研究の鍵となる。
三領域の比較分析——量子・古典・深層学習
意思決定・言語理解・概念形成にわたる三領域で、量子モデルを古典確率/ベイズモデルおよび深層学習と比較すると、以下のような大まかな整理が可能だ。
計算資源の観点では、意思決定と概念形成の主流モデルは小〜中次元の線形代数で実装でき、古典的なコンピュータで十分にシミュレーション可能だ。密度行列を用いる言語モデルでは次元爆発の懸念があるが、近似を用いれば対応できる範囲も多い。量子ハードウェアが実際に必要になるのは、回路実装を伴うQNLPのみだ。
予測力の観点では、意思決定の順序効果がQQ equalityという事前制約を持つという点で、量子モデルは他の領域や他のモデルと比べて相対的に強い証拠基盤を持つ。言語はNLPベンチマーク中心で結果が依存度が高く、概念形成は古典データへの整合性は高いが新規予測の体系的検証が薄い。
解釈可能性の観点では、量子モデルは「位相・干渉・状態更新」という概念を通じて中程度の解釈可能性を持つが、心理学的解釈(干渉が注意配分なのか記憶検索なのかなど)との対応は未整理だ。古典ベイズは生成過程を記述しやすく解釈可能性が高い一方、深層学習は予測性能に優れるが解釈は追加手法に依存する。
まとめ——量子モデルの可能性と、今後の研究が問うべきこと
本記事を通じて明らかになったことを整理する。
量子(ライク)モデルは、「測定の順序・文脈・状態更新を伴う判断」を単一の確率公理系で扱える点で、古典確率・ベイズモデルとは異なる価値を持つ。特に意思決定分野では、QQ equalityという事前・パラメータフリーの強い制約が大規模データで支持されており、この点は証拠として相対的に堅牢だ。
言語理解における密度行列アプローチは、曖昧性の定量化と文脈による解消を形式化できる点が利点だが、NLPの成功が認知的妥当性を保証するわけではない。概念形成では過拡張・典型性の創発を干渉で説明できるが、モデルの自由度を抑えた検証設計が不可欠だ。
量子計算資源については、意思決定・概念形成の主流研究では原則不要であり、古典計算で十分対応できる。QNLPは量子優位の可能性を議論できる段階にあるが、現状では優位の条件を厳密化することが先決だ。
これらを総合すると、量子モデルの評価基準は「データへの当てはまり」ではなく「どれだけ強い事前制約を出せるか・代替理論と識別できるか」に移行しつつある。この方向性こそが、量子認知研究をより堅固な科学的基盤の上に置くための道筋となる。
コメント